题目内容
曲线y=e-2x+1在点(0,2)处的切线在x上的截距等于
- A.
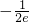
- B.

- C.1
- D.2e
C
分析:对函数求导数,再求x=0处的导数值,即得切线的斜率.利用点斜式写出切线的方程,再令y=0,即可求出切线在x上的截距的值.
解答:对y=e-2x+1求导数,得y'=-2e-2x,
∴当x=0时,y'=-2e0=-2
因此,曲线y=e-2x+1在点(0,2)处的切线斜率k=-2
∴切线方程为y-2=-2(x-0),即y=2-2x
令y=0得,x=1,故切线在x轴上的截距等于1
故选C
点评:本题给出一个特殊函数,求函数图象的切线在坐标轴上的截距,着重考查了导数的运算法则、利用导数研究函数图象和直线的截距等知识,属于基础题.
分析:对函数求导数,再求x=0处的导数值,即得切线的斜率.利用点斜式写出切线的方程,再令y=0,即可求出切线在x上的截距的值.
解答:对y=e-2x+1求导数,得y'=-2e-2x,
∴当x=0时,y'=-2e0=-2
因此,曲线y=e-2x+1在点(0,2)处的切线斜率k=-2
∴切线方程为y-2=-2(x-0),即y=2-2x
令y=0得,x=1,故切线在x轴上的截距等于1
故选C
点评:本题给出一个特殊函数,求函数图象的切线在坐标轴上的截距,着重考查了导数的运算法则、利用导数研究函数图象和直线的截距等知识,属于基础题.

练习册系列答案
相关题目
曲线y=e-2x+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |





