题目内容
过抛物线y2=x的焦点F的直线l的倾斜角θ≥A.(![]() ,1+
,1+![]() ) B.[
) B.[![]() ,1
,1![]()
C.[![]() ,1] D.(
,1] D.(![]() ,1)
,1)
解法一:如图所示.
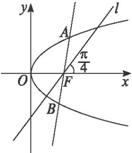
设A(x0,y0),焦点F(![]() ,0).
,0).
由抛物线的定义得|AF|=x0+![]() .
.
∴|AF|=x0+![]() .
.
当θ=![]() 时,直线AB:y-0=tan
时,直线AB:y-0=tan![]() (x-
(x-![]() ),即y=x-
),即y=x-![]() .
.
由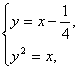 解得
解得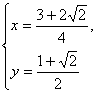 或
或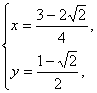
∵A在x轴上方,∴此时x0=![]() .
.
由图得,当θ≥![]() 时,0<x0≤
时,0<x0≤![]() .
.
∴![]() <|AF|≤
<|AF|≤![]() +
+![]() =1+
=1+![]() .
.
∴|AF|的取值范围是(![]() ,1+
,1+![]()
![]() .
.
故选A.
解法二:如图所示.
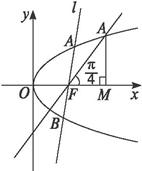
设A(x0,y0)(y0>0),焦点F(![]() ,0).
,0).
由抛物线定义得|AF|=x0+![]() =x0+
=x0+![]() .
.
当θ=![]() 时,过A作AM⊥x轴于M,
时,过A作AM⊥x轴于M,
则△AMF是等腰直角三角形.
∴此时x0=|OF|+|FM|=|OF|+|AM|=|OF|+y0.
∴此时有x0=![]() +y0.
+y0.
又∵y0=x0=-![]() ,又∵|AF|=
,又∵|AF|=![]() |AM|=
|AM|=![]() y0,
y0,
∴x0+![]() =
=![]() (x0-
(x0-![]() ).∴(
).∴(![]() -1)x0=
-1)x0=![]() .
.
∴此时x0=![]() =
=![]() .
.
∴当θ≥![]() 时,0<x0≤
时,0<x0≤![]() .
.
又∵|AF|=x0+![]() ,∴|AF|的取值范围是(
,∴|AF|的取值范围是(![]() ,1+
,1+![]()
![]() .故选A.
.故选A.
答案:A

练习册系列答案
相关题目
过抛物线y2=-x的焦点F的直线交抛物线于A、B两点,且A、B在直线x=
上的射影分别M,N,则∠MFN等于( )
| 1 |
| 4 |
| A、45° | B、60° |
| C、90° | D、以上都不对 |
已知过抛物线y2=x的焦点F的直线交抛物线于A、B两点,|AF|=
,则|BF|=( )
| 1 |
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|