题目内容
(2010•汕头模拟)若x∈(
,1),a=
,b=log
x,c=log2x,则 ( )
| 1 |
| 2 |
| 1 |
| 2x-2 |
| 1 |
| 2 |
分析:由于选择支中有且只有一个选项正确,故本选择题利用特殊值法解决即可.由x∈(
,1),取x=
,分别求出a,b,c的值,从而得出a,b,c的大小关系.
| 1 |
| 2 |
| ||
| 2 |
解答:解:由x∈(
,1),不妨取x=
,
则a=
=
=-
,
b=log
x=log
=
,
c=log2x=log2
=-
,
∵-
<-
<
,
∴a<c<b,
对照选项,知只有C正确.
故选C.
| 1 |
| 2 |
| ||
| 2 |
则a=
| 1 |
| 2x-2 |
| 1 | ||||
2×
|
2+
| ||
| 2 |
b=log
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
c=log2x=log2
| ||
| 2 |
| 1 |
| 2 |
∵-
2+
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a<c<b,
对照选项,知只有C正确.
故选C.
点评:本小题主要考查函数单调性的应用、对数函数的单调性与特殊点等基础知识,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
相关题目
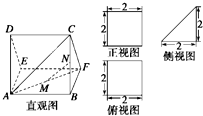 (2010•汕头模拟)如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点.
(2010•汕头模拟)如图,多面体AEDBFC的直观图及三视图如图所示,M,N分别为AF,BC的中点. (2010•汕头模拟)如图,在四边形ABCD中,设
(2010•汕头模拟)如图,在四边形ABCD中,设