题目内容
已知函数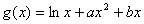 ,,函数
,,函数 的图象在点
的图象在点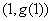 处的切线平行于
处的切线平行于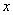 轴.
轴.
(1)确定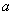 与
与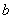 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意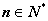 ,都有
,都有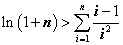 成立。
成立。
(1)依题意得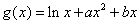 ,则
,则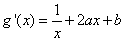
由函数 的图象在点
的图象在点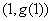 处的切线平行于
处的切线平行于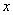 轴得:
轴得: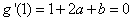
 ∴
∴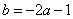
(2)由(1)得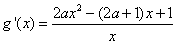
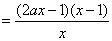 -
-
∵函数 的定义域为
的定义域为
∴①当 时,
时, 在
在 上恒成立,
上恒成立,
由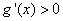 得
得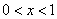 ,由
,由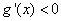 得
得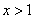 ,
,
即函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在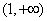 单调递减;-
单调递减;-
当 时,令
时,令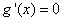 得
得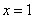 或
或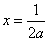 ,
,
②若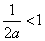 ,即
,即 时,由
时,由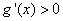 得
得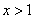 或
或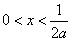 ,由
,由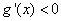 得
得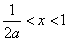 ,
,
即函数 在
在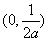 ,
,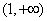 上单调递增,在
上单调递增,在 单调递减;
单调递减;
③若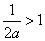 ,即
,即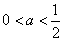 时,由
时,由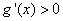 得
得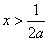 或
或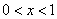 ,由
,由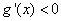 得
得 ,
,
即函数 在
在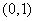 ,
,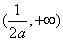 上单调递增,在
上单调递增,在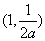 单调递减;-
单调递减;-
④若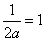 ,即
,即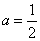 时,在
时,在 上恒有
上恒有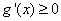 ,
,
即函数 在
在 上单调递增,
上单调递增,
综上得:当 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在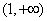 单调递减;
单调递减;
当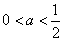 时,函数
时,函数 在
在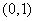 单调递增,在
单调递增,在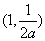 单调递减;在
单调递减;在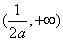 上单调递增;
上单调递增;
当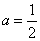 时,函数
时,函数 在
在 上单调递增,
上单调递增,
当 时,函数
时,函数 在
在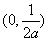 上单调递增,在
上单调递增,在 单调递减;在
单调递减;在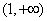 上单调递增.
上单调递增.
(3)证法一:由(2)知当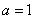 时,函数
时,函数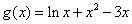 在
在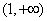 单调递增,
单调递增,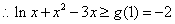 ,即
,即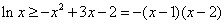 ,
,
令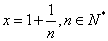 ,则
,则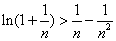 ,
,
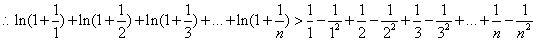
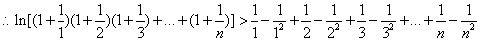
即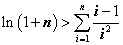
【证法二:构造数列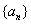 ,使其前
,使其前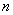 项和
项和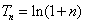 ,
,
则当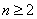 时,
时,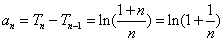 ,
,
显然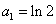 也满足该式,
也满足该式,
故只需证
令 ,即证
,即证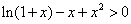 ,记
,记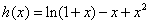 ,
,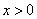
则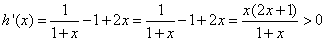 ,
,
 在
在 上单调递增,故
上单调递增,故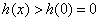 ,
,
∴ 成立,
成立,
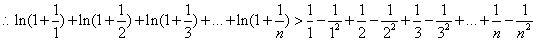
即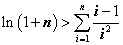 .
.
【证法三:令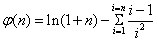 ,
,
则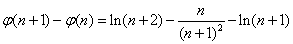
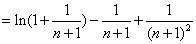 ----10分
----10分
令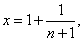 则
则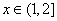 ,
,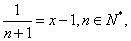
记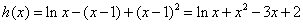 -
-
∵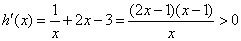 ∴函数
∴函数 在
在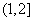 单调递增,
单调递增,
又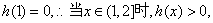 即
即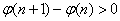 ,
,
∴数列 单调递增,又
单调递增,又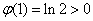 ,∴
,∴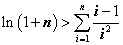

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
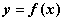 满足下列三个条件:
满足下列三个条件: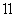 对任意的
对任意的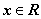 都有
都有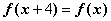 ;
; 对于任意的
对于任意的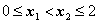 ,都有
,都有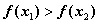 ;
;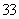
 的图象关于
的图象关于 轴对称. 则下列结论中,正确的是 ( )
轴对称. 则下列结论中,正确的是 ( )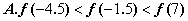
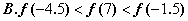
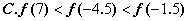
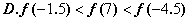
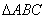 ,角A、B、C所对的边分别为
,角A、B、C所对的边分别为 ,若
,若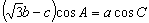 ,则
,则 =
=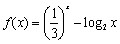 ,正实数
,正实数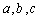 是公差为正数的等差数列,且满足
是公差为正数的等差数列,且满足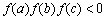 .若实数
.若实数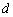 是方程
是方程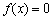 的一个解,那么下列四个判断:①
的一个解,那么下列四个判断:①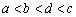 ;②
;②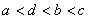 ;③
;③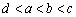 ;④
;④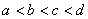 中有可能成立的个数为 ( )
中有可能成立的个数为 ( )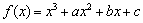 ,若
,若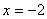 时,
时,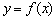 有极值.
有极值.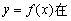
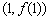 处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为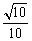 .
.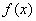 的解析式。
的解析式。 的图像与直线
的图像与直线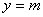 有三个不同的公共点,求实数
有三个不同的公共点,求实数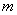 的取值范围.
的取值范围. 的定义域为
的定义域为 ,且
,且 是奇函数,
是奇函数, 是偶函数,学科网则下列结论中正确的是
是偶函数,学科网则下列结论中正确的是 是偶函数 B.
是偶函数 B.  是奇函数
是奇函数  是奇函数 D.
是奇函数 D.  是奇函数
是奇函数 ,若
,若 ,且
,且 ,则
,则 的取值 范围是
的取值 范围是 (B)
(B) (C)
(C) (D)
(D)
 .
.
 .
.
 .
.
 .
.
 的准线方程是( )
的准线方程是( ) B.
B.  C.
C.  D.
D. 