题目内容

△ABC的三个内角A，B，C满足sinA•cos² $数学公式$ +sinC•cos² $数学公式$ = $数学公式$ sinB，则cosB的取值范围是________．

$\text{[math]}$
分析：通过逆应用二倍角公式，化简方程，然后利用两角和的正弦函数、三角形的内角和，推出a、b、c关系，再利用余弦定理和基本不等式求出cosB的不等式，利用余弦函数的单调性求cosB的取值范围即可．
解答：由sinA•cos² $\text{[math]}$ +sinC•cos² $\text{[math]}$ = $\text{[math]}$ sinB，
可得sinA• 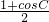$\text{[math]}$ +sinC• 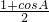$\text{[math]}$ = $\text{[math]}$ sinB
得：sinA+sinAcosC+sinC+sinCcosA=3sinB，
即sinA+sin（A+C）+sinC=3sinB，
∴sinA+sinC=2sinB，即2b=a+c．
由余弦定理，得：cosB= $\text{[math]}$
= $\text{[math]}$
= $\text{[math]}$
≥ $\text{[math]}$
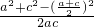
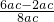
= $\text{[math]}$ ，当且仅当a=c时取等号，
∵cosx＜1，
所以cosB的范围是[ $\text{[math]}$ ，1）．
故答案为： $\text{[math]}$
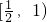
点评：本题是中档题，考查正弦定理．余弦定理、两角和的正弦函数的应用，基本不等式的应用，难度较大，考查计算能力．

练习册系列答案

新教材同步练系列答案

魔力一卷通系列答案

初中生期末大考卷系列答案

百年学典课时学练测系列答案

成功一号名卷天下优化测试卷系列答案

好学生课堂达标系列答案

随堂10分钟系列答案

集优方案系列答案

仁爱英语同步练习册系列答案

巴蜀学案同步导学系列答案

相关题目

已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=

，A+C=2B，则sinC=（　　）

△ABC的三个内角A、B、C的对边分别是a，b，c，给出下列命题：
①若sinBcosC＞-cosBsinC，则△ABC一定是钝角三角形；
②若sin²A+sin²B=sin²C，则△ABC一定是直角三角形；
③若bcosA=acosB，则△ABC为等腰三角形；
④在△ABC中，若A＞B，则sinA＞sinB；
其中正确命题的序号是

．（注：把你认为正确的命题的序号都填上）

已知△ABC的三个内角A，B，C的对边分别为a，b，c，且a，b，c成等比数列
（1）若sinC=2sinA，求cosB的值；
（2）求角B的最大值．并判断此时△ABC的形状．

已知a，b，c分别为△ABC的三个内角A，B，C的对边，

=(cosA，1)，且

．
（Ⅰ）求角A的大小；
（Ⅱ）若a=2，△ABC的面积为

已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=

，B=60°，则sinC=