题目内容
已知:如图所示,从Rt△ABC的两直角边AB,AC向外作正方形ABFG及ACDE,CF,BD分别交AB,AC于P,Q.求证:AP=AQ.

∵∠BAC+∠BAG=90°+90°=180°,
∴C,A,G三点共线.同理B,A,E三点共线.
∵AB∥GF,AC∥ED,∴ =
= ,
, =
= ,
,
即AP= ,AQ=
,AQ= .
.
又∵CA=ED=AE,GF=BA=AG,
∴CG=CA+AG=AE+BA=BE.
∴AP=AQ.
∴C,A,G三点共线.同理B,A,E三点共线.
∵AB∥GF,AC∥ED,∴
 =
= ,
, =
= ,
,即AP=
 ,AQ=
,AQ= .
.又∵CA=ED=AE,GF=BA=AG,
∴CG=CA+AG=AE+BA=BE.
∴AP=AQ.
证明 ∵∠BAC+∠BAG=90°+90°=180°,
∴C,A,G三点共线.同理B,A,E三点共线.
∵AB∥GF,AC∥ED,∴ =
= ,
, =
= ,
,
即AP= ,AQ=
,AQ= .
.
又∵CA=ED=AE,GF=BA=AG,
∴CG=CA+AG=AE+BA=BE.
∴AP=AQ.
∴C,A,G三点共线.同理B,A,E三点共线.
∵AB∥GF,AC∥ED,∴
 =
= ,
, =
= ,
,即AP=
 ,AQ=
,AQ= .
.又∵CA=ED=AE,GF=BA=AG,
∴CG=CA+AG=AE+BA=BE.
∴AP=AQ.

练习册系列答案
相关题目
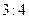 ,则它们的三角形面积比是____________.
,则它们的三角形面积比是____________.


 的对称点在
的对称点在 X轴上,则k是( ▲ )
X轴上,则k是( ▲ )




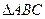 中,
中,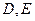 分别为
分别为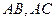 上的点,且
上的点,且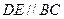 ,
,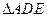 的面积是
的面积是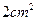 ,梯形
,梯形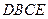 的面积为
的面积为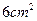 ,则
,则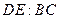 的值为( )
的值为( ) 


