题目内容
设函数f(x)=x·2x+x,A0为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量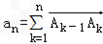 ,i=(1,0),设θn为an与i的夹角,则
,i=(1,0),设θn为an与i的夹角,则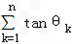 =( )
=( )
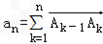 ,i=(1,0),设θn为an与i的夹角,则
,i=(1,0),设θn为an与i的夹角,则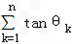 =( )
=( )2n+1+n﹣2

练习册系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|