题目内容
在△ABC中,内角A,B,C所对边长分别为a,b,c,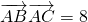 ,∠BAC=θ,a=4.
,∠BAC=θ,a=4.
(1)求b•c的最大值及θ的取值范围;
(2)求函数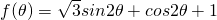 的最大值和最小值.
的最大值和最小值.
解(1)bc•cosθ=8,b2+c2-2bccosθ=42即b2+c2=32…(2分)
又b2+c2≥2bc所以bc≤16,即bc的最大值为16 …(4分)
即 所以
所以  ,又0<θ<π所以0<θ
,又0<θ<π所以0<θ …(6分)
…(6分)
(2)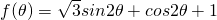 =
=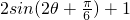 …(9分)
…(9分)
因0<θ ,所以
,所以 <
<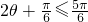 ,
,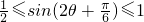 …(10分)
…(10分)
当 即
即 时,
时,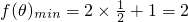 …(11分)
…(11分)
当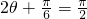 即
即 时,f(θ)max=2×1+1=3…(12分)
时,f(θ)max=2×1+1=3…(12分)
分析:(1)向量的数量积,利用余弦定理求出b2+c2=32,通过基本不等式求b•c的最大值及θ的取值范围;
(2)利用二倍角的正弦函数化简函数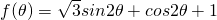 为一个角的三角函数的形式,通过角的范围正弦函数的最值求出函数的最大值和最小值.
为一个角的三角函数的形式,通过角的范围正弦函数的最值求出函数的最大值和最小值.
点评:本题考查三角函数的化简求值,余弦定理的应用,掌握正弦函数的基本性质,是解好本题的关键.
又b2+c2≥2bc所以bc≤16,即bc的最大值为16 …(4分)
即
 所以
所以  ,又0<θ<π所以0<θ
,又0<θ<π所以0<θ …(6分)
…(6分)(2)
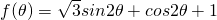 =
=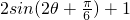 …(9分)
…(9分)因0<θ
 ,所以
,所以 <
<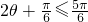 ,
,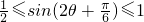 …(10分)
…(10分)当
 即
即 时,
时,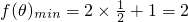 …(11分)
…(11分)当
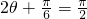 即
即 时,f(θ)max=2×1+1=3…(12分)
时,f(θ)max=2×1+1=3…(12分)分析:(1)向量的数量积,利用余弦定理求出b2+c2=32,通过基本不等式求b•c的最大值及θ的取值范围;
(2)利用二倍角的正弦函数化简函数
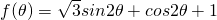 为一个角的三角函数的形式,通过角的范围正弦函数的最值求出函数的最大值和最小值.
为一个角的三角函数的形式,通过角的范围正弦函数的最值求出函数的最大值和最小值.点评:本题考查三角函数的化简求值,余弦定理的应用,掌握正弦函数的基本性质,是解好本题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目