ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΓΨ2017―ο÷ί“ΜΡΘΓΩ»γΆΦΘ§ΨΊ–ΈABCD «“ΜΗωάζ ΖΈΡΈο’ΙάάΧϋΒΡΗ© ”ΆΦΘ§ΒψE‘ΎAB…œΘ§‘ΎΧί–ΈBCDE«χ”ρΡΎ≤Ω’Ι ΨΈΡΈοΘ§DE «≤ΘΝßΡΜ«ΫΘ§”ΈΩΆ÷ΜΡή‘Ύ![]() ADE«χ”ρΡΎ≤ΈΙέΘ°‘ΎAE…œΒψP¥ΠΑ≤ΉΑ“ΜΩ…–ΐΉΣΒΡΦύΩΊ…ψœώΆΖΘ§
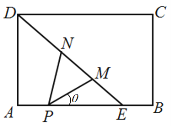
ADE«χ”ρΡΎ≤ΈΙέΘ°‘ΎAE…œΒψP¥ΠΑ≤ΉΑ“ΜΩ…–ΐΉΣΒΡΦύΩΊ…ψœώΆΖΘ§![]() ΈΣΦύΩΊΫ«Θ§Τδ÷–MΓΔN‘ΎœΏΕΈDEΘ®Κ§ΕΥΒψΘ©…œΘ§«“ΒψM‘ΎΒψNΒΡ”“œ¬ΖΫ.Ψ≠≤βΝΩΒΟ÷ΣΘΚAD=6ΟΉΘ§AE=6ΟΉΘ§AP=2ΟΉΘ§
ΈΣΦύΩΊΫ«Θ§Τδ÷–MΓΔN‘ΎœΏΕΈDEΘ®Κ§ΕΥΒψΘ©…œΘ§«“ΒψM‘ΎΒψNΒΡ”“œ¬ΖΫ.Ψ≠≤βΝΩΒΟ÷ΣΘΚAD=6ΟΉΘ§AE=6ΟΉΘ§AP=2ΟΉΘ§![]() .Φ«
.Φ«![]() Θ®ΜΓΕ»Θ©Θ§ΦύΩΊ…ψœώΆΖΒΡΩ… ”«χ”ρ
Θ®ΜΓΕ»Θ©Θ§ΦύΩΊ…ψœώΆΖΒΡΩ… ”«χ”ρ![]() PMNΒΡΟφΜΐΈΣSΤΫΖΫΟΉΘ°
PMNΒΡΟφΜΐΈΣSΤΫΖΫΟΉΘ°
Θ®1Θ©«σSΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ω
ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΘΜΘ®≤ΈΩΦ ΐΨίΘΚ
ΒΡ»Γ÷ΒΖΕΈßΘΜΘ®≤ΈΩΦ ΐΨίΘΚ![]() Θ©
Θ©
Θ®2Θ©«σ![]() ΒΡΉν–Γ÷Β.
ΒΡΉν–Γ÷Β.
ΓΨ¥πΑΗΓΩΦϊΫβΈω
ΓΨΫβΈωΓΩΔ≈ΖΫΖ®“ΜΘΚ‘Ύ![]() PME÷–Θ§
PME÷–Θ§![]() Θ§PE=AE-AP=4ΟΉΘ§
Θ§PE=AE-AP=4ΟΉΘ§![]() Θ§
Θ§![]() Θ§
Θ§
”…’ΐœ“Ε®άμΒΟ![]() Θ§
Θ§
Υυ“‘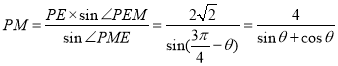 Θ§---------------------2Ζ÷
Θ§---------------------2Ζ÷
Ά§άμ‘Ύ![]() PNE÷–Θ§”…’ΐœ“Ε®άμΒΟ
PNE÷–Θ§”…’ΐœ“Ε®άμΒΟ![]() Θ§
Θ§
Υυ“‘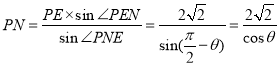 Θ§---------------------4Ζ÷
Θ§---------------------4Ζ÷
Υυ“‘![]() PMNΒΡΟφΜΐS
PMNΒΡΟφΜΐS![]()
![]()
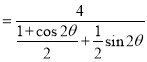
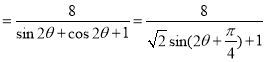 Θ§--------------------8Ζ÷
Θ§--------------------8Ζ÷
Β±M”κE÷ΊΚœ ±Θ§![]() ΘΜΒ±N”κD÷ΊΚœ ±Θ§
ΘΜΒ±N”κD÷ΊΚœ ±Θ§![]() ,Φ¥
,Φ¥![]() Θ§
Θ§![]() Θ§
Θ§
Υυ“‘![]() .
.
Ήέ…œΩ…ΒΟΘΚ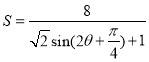 ,
,![]() .---------------------10Ζ÷
.---------------------10Ζ÷
ΖΫΖ®ΕΰΘΚ‘Ύ![]() PME÷–Θ§
PME÷–Θ§![]() Θ§PE=AE-AP=4ΟΉΘ§
Θ§PE=AE-AP=4ΟΉΘ§![]() Θ§
Θ§![]() Θ§”…’ΐœ“Ε®άμΩ…÷ΣΘΚ
Θ§”…’ΐœ“Ε®άμΩ…÷ΣΘΚ![]() Θ§
Θ§
Υυ“‘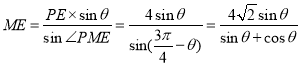 Θ§---------------------2Ζ÷
Θ§---------------------2Ζ÷
‘Ύ![]() PNE÷–Θ§”…’ΐœ“Ε®άμΩ…÷ΣΘΚ
PNE÷–Θ§”…’ΐœ“Ε®άμΩ…÷ΣΘΚ![]() Θ§
Θ§
Υυ“‘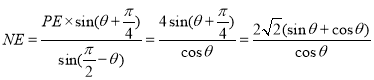 Θ§---------------------4Ζ÷
Θ§---------------------4Ζ÷
Υυ“‘![]() ,
,
”÷ΒψPΒΫDEΒΡΨύάκΈΣ![]() Θ§---------------------6Ζ÷
Θ§---------------------6Ζ÷
Υυ“‘![]() PMNΒΡΟφΜΐS=
PMNΒΡΟφΜΐS=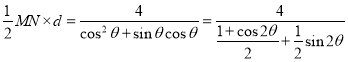
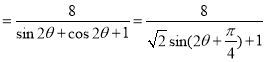 Θ§---------------------8Ζ÷
Θ§---------------------8Ζ÷
Β±M”κE÷ΊΚœ ±Θ§![]() ΘΜΒ±N”κD÷ΊΚœ ±Θ§
ΘΜΒ±N”κD÷ΊΚœ ±Θ§![]() ,Φ¥
,Φ¥![]() Θ§
Θ§![]() Θ§
Θ§
Υυ“‘![]() .
.
Ήέ…œΩ…ΒΟΘΚ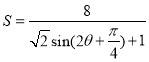 ,
,![]() .---------------------10Ζ÷
.---------------------10Ζ÷
ΔΤΒ±![]() Φ¥
Φ¥![]() ±Θ§
±Θ§![]() »ΓΒΟΉν–Γ÷ΒΈΣ
»ΓΒΟΉν–Γ÷ΒΈΣ![]() .---------13Ζ÷
.---------13Ζ÷
Υυ“‘Ω… ”«χ”ρ![]() PMNΟφΜΐΒΡΉν–Γ÷ΒΈΣ
PMNΟφΜΐΒΡΉν–Γ÷ΒΈΣ![]() ΤΫΖΫΟΉ.---------------------14Ζ÷
ΤΫΖΫΟΉ.---------------------14Ζ÷

 άΦΆΑΌΆ®”≈ΝΖ≤βœΒΝ–¥πΑΗ
άΦΆΑΌΆ®”≈ΝΖ≤βœΒΝ–¥πΑΗ ΑΌΖ÷―ß…ζΉς“Β±ΨΧβΝΖΆθœΒΝ–¥πΑΗ
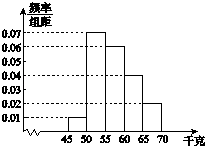
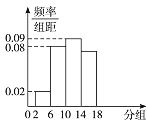
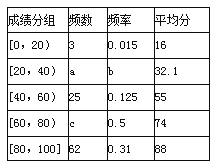
ΑΌΖ÷―ß…ζΉς“Β±ΨΧβΝΖΆθœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ‘ΎΡ≥¥Έ≤β―ι÷–Θ§”–6ΈΜΆ§―ßΒΡΤΫΨυ≥…Φ®ΈΣ75Ζ÷Θ°”Οxn±μ Ψ±ύΚ≈ΈΣnΘ®n=1Θ§2Θ§Γ≠Θ§6Θ©ΒΡΆ§―ßΥυΒΟ≥…Φ®Θ§«“«Α5ΈΜΆ§―ßΒΡ≥…Φ®»γœ¬ΘΚ
±ύΚ≈n | 1 | 2 | 3 | 4 | 5 |
≥…Φ®xn | 70 | 76 | 72 | 70 | 72 |
Θ®1Θ©«σΒΎ6ΈΜΆ§―ßΒΡ≥…Φ®x6 Θ§ ΦΑ’β6ΈΜΆ§―ß≥…Φ®ΒΡ±ξΉΦ≤νsΘΜ
Θ®2Θ©¥”«Α5ΈΜΆ§―ß÷–Θ§ΥφΜζΒΊ―Γ2ΈΜΆ§―ßΘ§«σ«Γ”–1ΈΜΆ§―ß≥…Φ®‘Ύ«χΦδΘ®68Θ§75Θ©÷–ΒΡΗ≈¬ Θ°