题目内容
设f(x)=3ax2+2bx+c(a≠0),若a+b+c=0,f(0)f(1)>0,求证:(1)方程f(x)=0有实数根;
(2)-2<
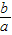 <-1;
<-1;(3)设x1,x2是方程f(x)=0的两个实数根,则
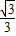 ≤|x1-x2|
≤|x1-x2|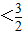 .
.
【答案】分析:(1)根据已知中a+b+c=0,利用配方法求出二次方程f(x)=0的△>0,即可判断出方程f(x)=0有实数根;
(2)由a+b+c=0,f(0)f(1)>0,我们可构造关于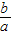 的不等式,解不等式可得)-2<
的不等式,解不等式可得)-2<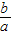 <-1;
<-1;
(3)当x1,x2是方程f(x)=0的两个实数根时,根据韦达定理我们可以求出,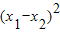 =
=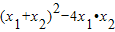 的范围,开方后可得
的范围,开方后可得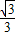 ≤|x1-x2|
≤|x1-x2|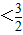 .
.
解答:解:(1)∵a≠0,a+b+c=0,a+c=-b,
∴△=4b2-12ac=4(a+c)2-12ac=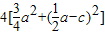 >0
>0
f(x)=3ax2+2bx+c=0有实数根,--(4分)
(2)由f(0)f(1)>0,得c(3a+2b+c)>0
∵a+b+c=0,
∴c=-(a+b),
∴-(a+b)•(2a+b)>0,
∴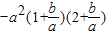 >0,
>0,
∴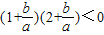
解得-2<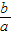 <-1----------(9分)
<-1----------(9分)
(3)∵x1,x2是方程f(x)=0的两个实数根,
∴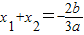 ,
,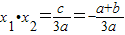
∴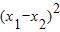 =
=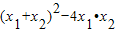
=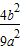 -4(
-4(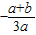 )
)
=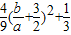
∵-2<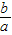 <-1
<-1
∴ <
<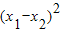 <
<
∴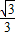 ≤|x1-x2|
≤|x1-x2|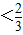 .--------(15分)
.--------(15分)
点评:本题考查的知识点是二次函数的性质,方程的根,韦达定理,是函数、方程与不等式之间相互关系的典型例题.
(2)由a+b+c=0,f(0)f(1)>0,我们可构造关于
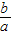 的不等式,解不等式可得)-2<
的不等式,解不等式可得)-2<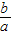 <-1;
<-1;(3)当x1,x2是方程f(x)=0的两个实数根时,根据韦达定理我们可以求出,
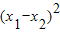 =
=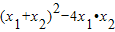 的范围,开方后可得
的范围,开方后可得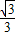 ≤|x1-x2|
≤|x1-x2|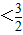 .
.解答:解:(1)∵a≠0,a+b+c=0,a+c=-b,
∴△=4b2-12ac=4(a+c)2-12ac=
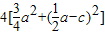 >0
>0f(x)=3ax2+2bx+c=0有实数根,--(4分)
(2)由f(0)f(1)>0,得c(3a+2b+c)>0
∵a+b+c=0,
∴c=-(a+b),
∴-(a+b)•(2a+b)>0,
∴
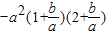 >0,
>0,∴
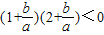
解得-2<
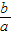 <-1----------(9分)
<-1----------(9分)(3)∵x1,x2是方程f(x)=0的两个实数根,
∴
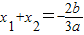 ,
,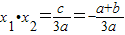
∴
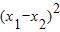 =
=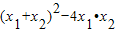
=
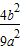 -4(
-4(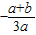 )
)=
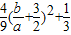
∵-2<
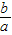 <-1
<-1∴
 <
<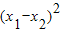 <
<
∴
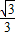 ≤|x1-x2|
≤|x1-x2|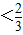 .--------(15分)
.--------(15分)点评:本题考查的知识点是二次函数的性质,方程的根,韦达定理,是函数、方程与不等式之间相互关系的典型例题.

练习册系列答案
相关题目