题目内容
等比数列 的首项为
的首项为 ,公比为
,公比为 ,用
,用 表示这个数列的第n项到第m项共
表示这个数列的第n项到第m项共 项的和.
项的和.
(Ⅰ)计算 ,
, ,
, ,并证明它们仍成等比数列;
,并证明它们仍成等比数列;
(Ⅱ)受上面(Ⅰ)的启发,你能发现更一般的规律吗?写出你发现的一般规律,并证明.
(Ⅰ)证明(略);(Ⅱ)
解析试题分析:等比数列的判定方法:(1)定义法:若 是常数,则
是常数,则 是等比数列;中项公式法:若数列
是等比数列;中项公式法:若数列 中,
中, ,则
,则 是等比数列;通项公式法:若数列通项公式可写成
是等比数列;通项公式法:若数列通项公式可写成 (2)通过观察个别情况发现某些相同本质,由特殊得出一般的结论
(2)通过观察个别情况发现某些相同本质,由特殊得出一般的结论
试题解析:(Ⅰ) ,
, ,
, 
因为 , 所以
, 所以 成等比数列.
成等比数列.
(Ⅱ)一般地 、
、 且m、n、p、r均为正整数)也成等比数列,
且m、n、p、r均为正整数)也成等比数列, ,
,  ,
, ,
, 

所以 成等比数列.
成等比数列.
考点:等比数列的判断及归纳推理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}是各项均为正数的等比数列,{bn}是等差数列,且a6=b7,则有
| A.a3+a9<b4+b10 |
| B.a3+a9≥b4+b10 |
| C.a3+a9≠b4+b10 |
| D.a3+a9与b4+b10的大小不确定 |
等比数列 的首项
的首项 ,前
,前 项和为
项和为 若
若 ,则公比
,则公比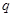 等于 ( )
等于 ( )
A. | B.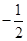 | C.2 | D.-2 |
在数列 中,
中, (c为非零常数)且前n项和
(c为非零常数)且前n项和 ,则实数k等于( ).
,则实数k等于( ).
A.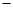 1 1 | B.1 | C.0 | D.2 |
已知函数 ,则
,则 ,
,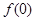 ,
, 的大小关系是
的大小关系是
A. | B. |
C. | D. |
已知 ,下列命题正确的是
,下列命题正确的是
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则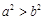 | D.若 ,则 ,则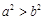 |
 中,
中, ,D是AC上一点,E是BC上一点,若
,D是AC上一点,E是BC上一点,若 .
. ,
, ,则BC= .
,则BC= .
 ,则
,则 .
.
