题目内容
(本小题满分14分)已知数列 和
和 满足
满足 ,
, ,
, 。
。
(1)求证:数列 为等差数列,并求数列
为等差数列,并求数列 通项公式;
通项公式;
(2) 数列 的前
的前 项和为
项和为 ,令
,令 ,求
,求 的最小值。
的最小值。
 和
和 满足
满足 ,
, ,
, 。
。(1)求证:数列
 为等差数列,并求数列
为等差数列,并求数列 通项公式;
通项公式;(2) 数列
 的前
的前 项和为
项和为 ,令
,令 ,求
,求 的最小值。
的最小值。(1)作差再同除以 ,即可证明
,即可证明 为等差数列,
为等差数列,
(2)最小值为
 ,即可证明
,即可证明 为等差数列,
为等差数列,
(2)最小值为

试题分析:(1)

 ,
, ,即
,即 , ……4分
, ……4分 数列
数列 是公差为1,首项为1等差数列. ……5分
是公差为1,首项为1等差数列. ……5分 即
即
 即
即 . ……7分
. ……7分(2)
 =
= , ……9分
, ……9分因为
 ,
,所以
 单调递增, ……12分
单调递增, ……12分 ,
,  的最小值为
的最小值为 . ……14分
. ……14分点评:由递推关系式求通项公式时一般都再写一个作差,然后用累加、累乘或构造新数列解决问题.而数列求和也是高考必考的一个内容,要好好掌握.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 而言,若
而言,若 是以
是以 为公差的等差数列,
为公差的等差数列,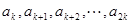 是以
是以 为公差的等差数列,依此类推,我们就称该数列为等差数列接龙,已知
为公差的等差数列,依此类推,我们就称该数列为等差数列接龙,已知 ,则
,则 等于
等于 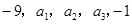 五个实数成等差数列,
五个实数成等差数列,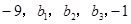 五个实数成等比数列,则
五个实数成等比数列,则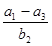 等于 ( )
等于 ( )




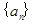 的前
的前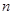 项和
项和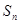 ,
,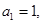
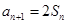 .
.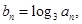 求数列
求数列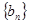 的前
的前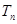 .
. 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 都在函数
都在函数 的图像上.
的图像上. 的通项公式;
的通项公式; ,求数列
,求数列 的通项公式.
的通项公式.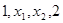 成等差数列,
成等差数列,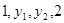 成等比数列,则
成等比数列,则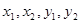 的大小关系是( )
的大小关系是( )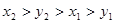

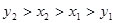
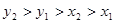
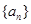 的前
的前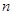 项和
项和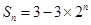 ,则
,则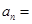 .
.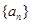 的前
的前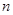 项和
项和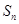 满足
满足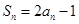 ,等差数列
,等差数列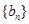 满足
满足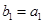 ,
,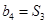 。
。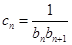 ,数列
,数列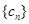 的前
的前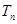 ,问
,问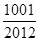 的最小正整数
的最小正整数 的前
的前 项和为
项和为 ,若
,若 ,则
,则 = 。
= 。