题目内容
在△ABC中,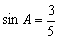 ,
,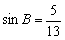 ,求cosC的值并判断△ABC的形状。
,求cosC的值并判断△ABC的形状。
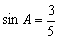 ,
,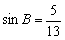 ,求cosC的值并判断△ABC的形状。
,求cosC的值并判断△ABC的形状。解:由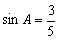 ,可得
,可得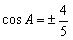 ,
,
由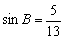 ,可得
,可得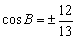 ,
,
因为A、B至多一个钝角,因此,cosA,cosB至多有一个小于零,
(Ⅰ)当A、B均为锐角时,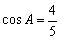 ,
,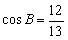 ,
,
所以,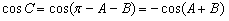
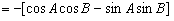
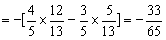 ,
,
所以,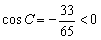 ,△ABC为钝角三角形。
,△ABC为钝角三角形。
(Ⅱ)当A为钝角,B为锐角时,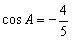 ,
,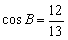 ,
,
所以,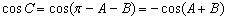
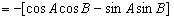
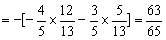 ,
,
所以,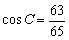 ,
,
又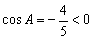 ,△ABC为钝角三角形。
,△ABC为钝角三角形。
(Ⅲ)当B为钝角,A为锐角时,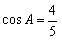 ,
,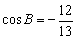 ,
,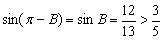 ,且
,且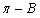 ,
,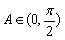 ,
,
所以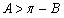 ,从而
,从而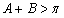 ,矛盾,从而B为钝角,A为锐角不成立。
,矛盾,从而B为钝角,A为锐角不成立。
综上所述,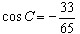 或
或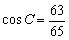 ,△ABC为钝角三角形。
,△ABC为钝角三角形。

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ABC中,设
ABC中,设 ,求A的值。
,求A的值。 ,求角
,求角 大小
大小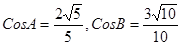 求:
求: ,求△ABC的面积。
,求△ABC的面积。 ABC中,设
ABC中,设 ,求A的值。
,求A的值。