题目内容
(本小题满分12分)
如图,在直三棱柱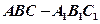 中,
中,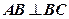 ,
,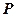 为
为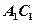 的中点,且
的中点,且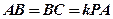 ,
,
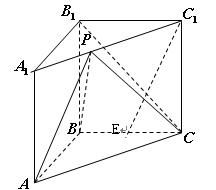
(1)当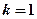 时,求证:
时,求证: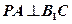 ;
;
(2)若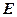 为
为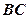 中点,当
中点,当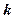 为何值时,异面直线
为何值时,异面直线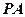
与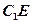 所成的角的正弦值为
所成的角的正弦值为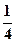 。
。
如图,在直三棱柱
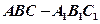 中,
中,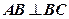 ,
,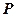 为
为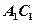 的中点,且
的中点,且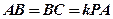 ,
,
(1)当
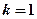 时,求证:
时,求证: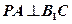 ;
;(2)若
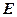 为
为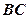 中点,当
中点,当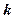 为何值时,异面直线
为何值时,异面直线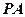
与
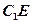 所成的角的正弦值为
所成的角的正弦值为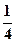 。
。略
(1)(方法一)连结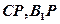 ,因为
,因为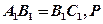 为
为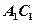 中点,
中点,
所以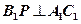 ,
,
又 因为面
因为面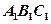
 面
面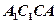 ,
,
所以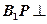 面
面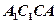 ,所以
,所以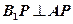 ;
;
设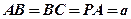 ,则
,则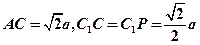 ,所以
,所以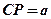 ,
,
所以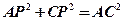 ,所以
,所以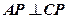 ,
,
又因为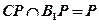
 ,
,
所以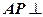 面
面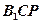 ,所以
,所以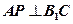 ....6
....6
(方法二)设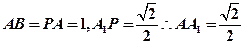 , 如图建系,
, 如图建系,
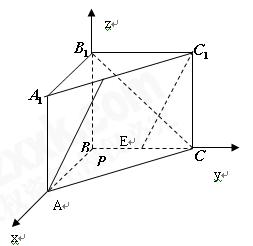
则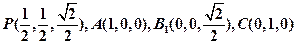 ,
,
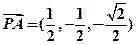 ,
,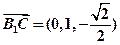
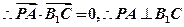 ......6
......6
(2)(方法一)取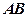 中点
中点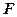 ,连结
,连结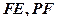 ,
,
因为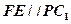 且
且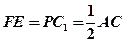 ,所以四边形
,所以四边形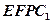 为平行四边形,
为平行四边形,
所以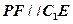 ,所以
,所以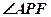 为异面直线
为异面直线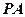 与
与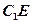 所成的角
所成的角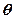 ;......8
;......8
设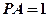 ,则
,则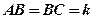 ,求得
,求得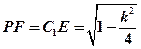 ,
,
所以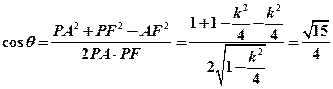 ,
,
解得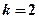 (舍)或
(舍)或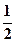 。......12
。......12
(方法二)设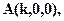 ,
,
则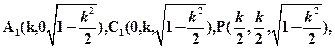
所以
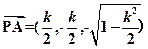 ,
,
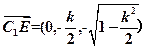 , ......8
, ......8
所以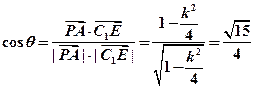 ,
,
所以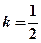 ......12
......12
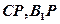 ,因为
,因为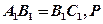 为
为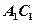 中点,
中点,所以
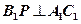 ,
,又
 因为面
因为面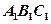
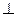 面
面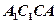 ,
,所以
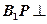 面
面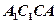 ,所以
,所以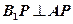 ;
;
|
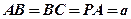 ,则
,则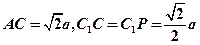 ,所以
,所以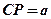 ,
,所以
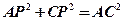 ,所以
,所以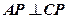 ,
,又因为
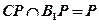
 ,
,
|
|
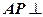 面
面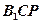 ,所以
,所以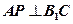 ....6
....6
|
|
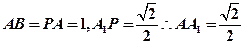 , 如图建系,
, 如图建系,
则
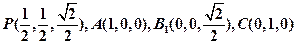 ,
,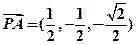 ,
,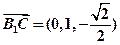
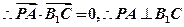 ......6
......6(2)(方法一)取
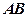 中点
中点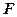 ,连结
,连结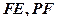 ,
,因为
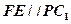 且
且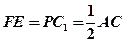 ,所以四边形
,所以四边形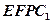 为平行四边形,
为平行四边形,所以
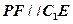 ,所以
,所以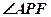 为异面直线
为异面直线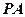 与
与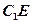 所成的角
所成的角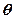 ;......8
;......8设
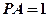 ,则
,则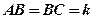 ,求得
,求得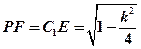 ,
,所以
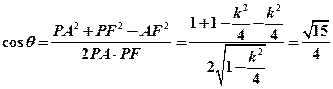 ,
,解得
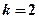 (舍)或
(舍)或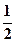 。......12
。......12(方法二)设
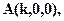 ,
,则
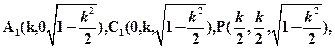
所以

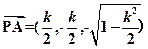 ,
,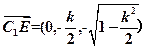 , ......8
, ......8所以
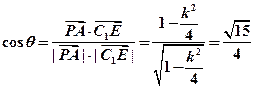 ,
,所以
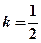 ......12
......12
练习册系列答案
相关题目
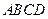 中,
中,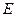 是
是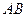 的中点,点
的中点,点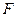 是
是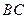 的中点,将
的中点,将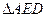 ,
,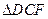 分别沿
分别沿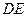 ,
,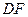 折起,使
折起,使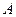 ,
,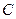 两点重合于点
两点重合于点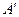 .求证:
.求证: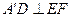 .
.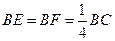 时,求三棱椎
时,求三棱椎 的体积.
的体积.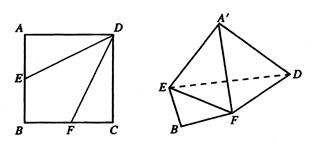
 中,底面
中,底面 是直角梯形,
是直角梯形,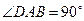 ,
,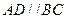 ,
,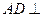 侧面
侧面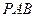 ,△
,△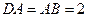 ,
, 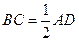 ,
,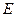 是线段
是线段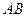 的中点.
的中点.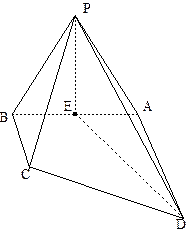
 ;
;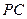 与平面
与平面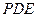 所成角的正弦值.
所成角的正弦值.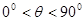
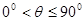
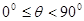
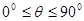
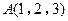 ,
,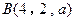 ,且
,且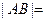
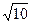 ,则
,则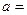 ( )
( )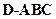 的外接球的球心O满足
的外接球的球心O满足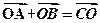 ,且外接球的体积为
,且外接球的体积为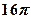 ,则该三棱锥的体积为 .
,则该三棱锥的体积为 . 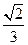
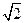
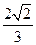
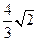
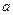 的正方体
的正方体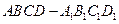 的8个顶点都在球
的8个顶点都在球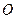 的表面上,E、F分别是棱
的表面上,E、F分别是棱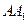 、
、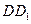 的中点,则直线EF被球
的中点,则直线EF被球 学
学