题目内容
已知向量
＝
，
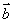＝(cos x，－1)．
(1)当向量∥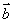时，求cos2x－sin 2x的值；
(2)设函数f(x)＝2(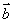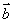＋)·，已知在△ABC中，内角A，B，C的对边分别为a，b，c，若a＝
，b＝2，sin B＝
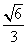，求f(x)＋4cos(2A＋
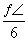)(x∈[0，
])的取值范围．
解 (1)∵a∥b，∴
cos x＋sin x＝0，∴tan x＝－.
∴cos2x－sin 2x＝
＝
＝
.
(2)f(x)＝2(a＋b)·b＝
sin
＋
，
由正弦定理
＝
，可得sin A＝
，∴A＝
.
∴f(x)＋4cos
＝sin－
，
∵x∈[0，]，∴2x＋∈[，
]．
∴
－1≤f(x)＋4cos(2A＋)≤－.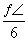
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
中，
是三角形的三内角，
，则该三角形是（ ）
，
，则
（ ）
B．
C．
D．
上到其焦点
距离为5的点有( )
，则此物体达到最高时的高度为（ ） 
B.
C.
D.
，sinx＋cosx≥2
，tanx＞sinx