题目内容
在△ABC中，∠A=30°，a=4，b=5，那么满足条件的△ABC（ ）A．无解
B．有 一个解
C．有两个解
D．不能确定
【答案】分析：根据余弦定理a2=b2+c2-2bccosA的式子，代入题中数据化简得c2-5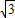
c+9=0，由根的判别式与韦达定理得到该方程有两个不相等的正实数根，由此可得△ABC有两个解．
解答：解：∵在△ABC中，∠A=30°，a=4，b=5，
∴由余弦定理a2=b2+c2-2bccosA，得
16=25+c2-10ccos30°，得c2-5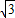
c+9=0（*）
∵△=（5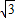
）2-4×1×9=39＞0，且两根之和、两根之积都为正数
∴方程（*）有两个不相等的正实数根，即有两个边c满足题中的条件
由此可得满足条件的△ABC有两个解
故选：C
点评：本题给出三角形的两条边和其中一边的对角，判断三角形解的个数．着重考查了利用余弦定理解三角形、一元二次方程根的判断式与韦达定理等知识，属于基础题．
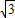c+9=0，由根的判别式与韦达定理得到该方程有两个不相等的正实数根，由此可得△ABC有两个解．解答：解：∵在△ABC中，∠A=30°，a=4，b=5，
∴由余弦定理a2=b2+c2-2bccosA，得
16=25+c2-10ccos30°，得c2-5
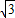c+9=0（*）∵△=（5
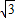）2-4×1×9=39＞0，且两根之和、两根之积都为正数∴方程（*）有两个不相等的正实数根，即有两个边c满足题中的条件
由此可得满足条件的△ABC有两个解
故选：C
点评：本题给出三角形的两条边和其中一边的对角，判断三角形解的个数．着重考查了利用余弦定理解三角形、一元二次方程根的判断式与韦达定理等知识，属于基础题．
练习册系列答案
相关题目