题目内容
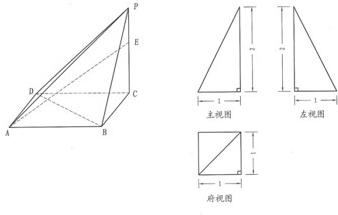
从物体的前面向后面投射所得的视图称主视图,从物体的上面向下面投射所得的视图称俯视图、从物体的左面向右面投射所得的视图称左视图已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点.
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD⊥AE?证明你的结论;
(Ⅲ)若E点为PC的中点,求二面角D-AE-B的大小.
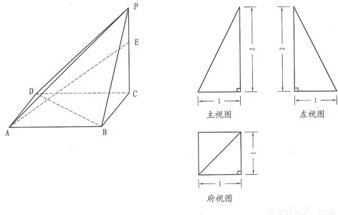
【答案】分析:(I)由三视图知PC⊥面ABCD,即高PC=2,且底面为正方形,边长为1,利用锥体体积公式计算即可.
(II)由于PC⊥BD,且BD⊥AC,所以不论点E在何位置,都有BD⊥面ACE,从而都有BD⊥AE.
(III)法一,连接AC,交BD于O.由对称性,二面角D-AE-B是二面角O-AE-B的2倍,利用射影面积法求出二面角O-AE-B的平面角后,问题获解
法二,以C为坐标原点,CD所在直线为x轴建立空间直角坐标系.求出平面ADE和平面ABE的法向量,利用向量的方法求出二面角D-AE-B的大小.
解答:
 解:(I)由三视图知PC⊥面ABCD,
解:(I)由三视图知PC⊥面ABCD,
ABCD为正方形,
且PC=2,AB=BC=1(2分)
∴VP-ABCD= •SABCD×PC=
•SABCD×PC= •12•2=
•12•2= (1分)
(1分)
(II)∵PC⊥面ABCD,BD?面ABCD
∴PC⊥BD …(1分)
而BD⊥AC,AC∩AE=A,
∴BD⊥面ACE,…(1分)
而AE?面ACE
∴BD⊥AE (1分)
(III)法一:连接AC,交BD于O.由对称性,二面角D-AE-B是二面角O-AE-B的2倍,设θ为二面角O-AE-B的平面角.
注意到B在面ACE上的射影为O
S△AOE= S△ACE=
S△ACE= ×
× ×
× =
= .
.
S△ABE= AB•BE=
AB•BE= •1•
•1• =
= ,(2分)
,(2分)
∴cosθ= =
=
∴θ=60°
∴二面角D-AE-B是120°(2分)
法二:以C为坐标原点,CD所在直线为x轴建立空间直角坐标系
则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),
从而 =(-1,0,1),
=(-1,0,1), =(0,1,0),
=(0,1,0),
 =(1,0,0),
=(1,0,0), =(0,-1,1)(2分)
=(0,-1,1)(2分)
设平面ADE和平面ABE的法向量分别为
 =(x1,y1,z1),
=(x1,y1,z1), =(x2,y2,z2)
=(x2,y2,z2)
则-x1+z1=0,y1=0
x2=0,-y2+z2=0
令z1=1,z2=-1,则
 =( (1,0,1),
=( (1,0,1), =(0,-1,-1)(2分)
=(0,-1,-1)(2分)
设二面角D-AE-B的平面角为θ,则|cosθ|= =
= =
= .
.
二面角D-AE-B为钝二面角.∴二面角D-AE-B的大小为 .(2分)
.(2分)
点评:本题考查几何体的三视图及直观图,线面垂直关系的判定,二面角的大小度量.考查考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.
(II)由于PC⊥BD,且BD⊥AC,所以不论点E在何位置,都有BD⊥面ACE,从而都有BD⊥AE.
(III)法一,连接AC,交BD于O.由对称性,二面角D-AE-B是二面角O-AE-B的2倍,利用射影面积法求出二面角O-AE-B的平面角后,问题获解
法二,以C为坐标原点,CD所在直线为x轴建立空间直角坐标系.求出平面ADE和平面ABE的法向量,利用向量的方法求出二面角D-AE-B的大小.
解答:

 解:(I)由三视图知PC⊥面ABCD,
解:(I)由三视图知PC⊥面ABCD,ABCD为正方形,
且PC=2,AB=BC=1(2分)
∴VP-ABCD=
 •SABCD×PC=
•SABCD×PC= •12•2=
•12•2= (1分)
(1分)(II)∵PC⊥面ABCD,BD?面ABCD
∴PC⊥BD …(1分)
而BD⊥AC,AC∩AE=A,
∴BD⊥面ACE,…(1分)
而AE?面ACE
∴BD⊥AE (1分)
(III)法一:连接AC,交BD于O.由对称性,二面角D-AE-B是二面角O-AE-B的2倍,设θ为二面角O-AE-B的平面角.
注意到B在面ACE上的射影为O
S△AOE=
 S△ACE=
S△ACE= ×
× ×
× =
= .
.S△ABE=
 AB•BE=
AB•BE= •1•
•1• =
= ,(2分)
,(2分)∴cosθ=
 =
=
∴θ=60°
∴二面角D-AE-B是120°(2分)
法二:以C为坐标原点,CD所在直线为x轴建立空间直角坐标系
则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),
从而
 =(-1,0,1),
=(-1,0,1), =(0,1,0),
=(0,1,0), =(1,0,0),
=(1,0,0), =(0,-1,1)(2分)
=(0,-1,1)(2分)设平面ADE和平面ABE的法向量分别为
 =(x1,y1,z1),
=(x1,y1,z1), =(x2,y2,z2)
=(x2,y2,z2)则-x1+z1=0,y1=0
x2=0,-y2+z2=0
令z1=1,z2=-1,则
 =( (1,0,1),
=( (1,0,1), =(0,-1,-1)(2分)
=(0,-1,-1)(2分)设二面角D-AE-B的平面角为θ,则|cosθ|=
 =
= =
= .
.二面角D-AE-B为钝二面角.∴二面角D-AE-B的大小为
 .(2分)
.(2分)点评:本题考查几何体的三视图及直观图,线面垂直关系的判定,二面角的大小度量.考查考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 随着某市精神文明建设的不断推进,市民八小时以外的时间越来越多,下面是某报记者在抽样调查了一些市民八小时以外用于读书的时间(单位:分钟)后,绘制的频数分布直方图,从左至右的前六个长方形所相对应的频率之和为0.95,最后一组的频数是10,则此次抽样调查的人数共有( )
随着某市精神文明建设的不断推进,市民八小时以外的时间越来越多,下面是某报记者在抽样调查了一些市民八小时以外用于读书的时间(单位:分钟)后,绘制的频数分布直方图,从左至右的前六个长方形所相对应的频率之和为0.95,最后一组的频数是10,则此次抽样调查的人数共有( )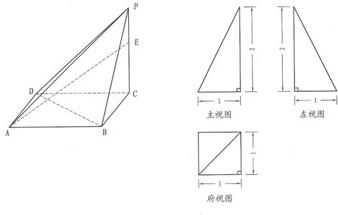
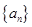 和等比数列
和等比数列 中,a1=2b1=2,b6=32,
中,a1=2b1=2,b6=32,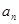 和
和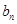 ;
;