题目内容
.某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40,50)，[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．
(1)求图中x的值；
(2)从成绩不低于80分的学生中随机选取2人，该2人中成绩在90分以上(含90分)的人数记为X，求X的分布列与数学期望．
解 (1)由频率分布直方图知(0.006×3＋0.01＋x＋0.054)×10＝1，解得x＝0.018.
(2)由频率分布直方图知成绩不低于80分的学生人数为(0.018＋0.006)×10×50＝12，成绩在90分以上(含90分)的人数为0.006×10×50＝3.
因此X可能取0,1,2三个值．
X的分布列为
| X | 0 | 1 | 2 |
| P |
|
|
|
练习册系列答案
相关题目
中国式过马路，是网友对部分中国人集体闯红灯现象的一种调侃，即“凑够一撮人就可以走了，和红绿灯无关”．某校对全校学生过马路方式进行调查，在所有参与调查的人中，“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示：
|
| 跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 |
| 男生 | 800 | 440 | 200 |
| 女生 | 200 | 160 | 200 |
(1)在所有参与调查的人中，用分层抽样的方法抽取n个人，已知“跟从别人闯红灯”的人中抽取50人，求n的值．
(2)在“带头闯红灯”的人中，将男生的200人编号为001,002，…，200；将女生的200人编号为201,202，…，400，用系统抽样的方法抽取5人参加“文明交通”宣传活动，若抽取的第一个人的编号为30，把抽取的5人看成一个总体，从这5人中任选取2人，求至少有一名女生的概率．
(n＝1,2,3,4)，其中a是常数，则
的值为( )
B.
C.
D.
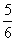
，则m的值是（ ）