题目内容
如图，已知P是⊙O外一点，PD为⊙O的切线，D为切点，割线PEF经过圆心O，若PF=12，PD=4| 3 |
分析：由PD为⊙O的切线结合切割线定理得PD2=PE•PF，代入数据即可求得圆O的半径长；再在直角三角形POD中，由OD=
PO可得∠P，最后利用圆周角与圆心角的关系即可求得∠EFD的度数．
| 1 |
| 2 |
解答：
解：由切割线定理得PD2=PE•PF
?PE=
=
=4
?EF=8，OD=4，利用
∵OD⊥PD，OD=
PO
∴∠P=30°，∠POD=60°，∠PDE=∠EFD=30°．
故答案为：4；30°．
解：由切割线定理得PD2=PE•PF?PE=
| PD2 |
| PF |
| 16×3 |
| 12 |
?EF=8，OD=4，利用
∵OD⊥PD，OD=
| 1 |
| 2 |
∴∠P=30°，∠POD=60°，∠PDE=∠EFD=30°．
故答案为：4；30°．
点评：本小题主要考查圆的切线的性质定理的证明、与圆有关的比例线段等基础知识，考查运算证明能力、化归与转化思想．属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
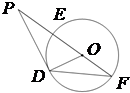（2013•河西区一模）（几何证明选做题）如图，已知P是⊙O外一点，PD为⊙O的切线，D为切点，割线PEF经过圆心O，若PF=12，PD=4
，则⊙O的半径长为 ．
，则圆O的半径长为 、∠EFD的度数为 ．
，则圆O的半径长为 、∠EFD的度数为 ．