题目内容
设数列{an}是等差数列,且a2=-8,a15=5,Sn是数列{an}的前n项和,则( )
| A、S10=S11 | B、S10>S11 | C、S9=S10 | D、S9<S10 |
分析:根据等差数列的两项的值,求出数列的公差,写出数列的通项,根据通项可以看出第十项的值等于0,得到前十项和前九项的和相等.
解答:解:∵a2=-8,a15=5,
设公差为d,则d=
=1,
∴an=n-10,
因此S9=S10是前n项和中的最小值,
选择C.
设公差为d,则d=
| 5+8 |
| 15-2 |
∴an=n-10,
因此S9=S10是前n项和中的最小值,
选择C.
点评:本题考查等差数列的性质,本题解题的关键是看出第十项等于0,本题也可以根据前n项之和的公式求解.

练习册系列答案
相关题目
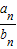 }的前n项和Sn.
}的前n项和Sn.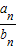 }的前n项和Sn.
}的前n项和Sn.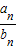 }的前n项和Sn.
}的前n项和Sn.