题目内容
19.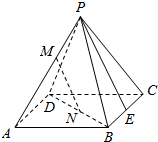 如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.
如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.(1)求证:直线MN∥平面PBC;
(2)若∠PAD=45°,且PD⊥平面ABCD,求异面直线MN,PD所成角的余弦值.
分析 (1)由已知得$\overrightarrow{MN}=\overrightarrow{MP}+\overrightarrow{PB}+\overrightarrow{BN}$=$\frac{1}{3}\overrightarrow{BC}$-$\frac{2}{3}\overrightarrow{BP}$,从而$\overrightarrow{MN}$与$\overrightarrow{BC}$,$\overrightarrow{BP}$共面,由此能证明MN∥平面BCP.
(2)以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出异面直线MN,PD所成角的余弦值.
解答 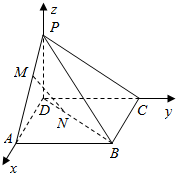 (1)证明:∵P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$,
(1)证明:∵P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$,
∴$\overrightarrow{MN}=\overrightarrow{MP}+\overrightarrow{PB}+\overrightarrow{BN}$
=-$\overrightarrow{PM}+\overrightarrow{PB}+\overrightarrow{BN}$
=-$\frac{1}{3}\overrightarrow{PA}$+$\overrightarrow{PB}$+$\frac{1}{3}\overrightarrow{BD}$
=-$\frac{1}{3}$($\overrightarrow{BA}-\overrightarrow{BP}$)+$\overrightarrow{PB}$+$\frac{1}{3}$($\overrightarrow{BA}+\overrightarrow{BC}$)
=$\frac{1}{3}\overrightarrow{BP}$-$\overrightarrow{BP}$+$\frac{1}{3}\overrightarrow{BC}$
=$\frac{1}{3}\overrightarrow{BC}$-$\frac{2}{3}\overrightarrow{BP}$,
∴$\overrightarrow{MN}$与$\overrightarrow{BC}$,$\overrightarrow{BP}$共面,
∴$\overrightarrow{MN}$∥平面BCP,
∵MN?平面BCP,∴MN∥平面BCP.
(2)解:∵∠PAD=45°,且PD⊥平面ABCD,
∴以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,
设AB=3,由已知得M(1,0,2),N(1,1,0),D(0,0,0),P(0,0,3),
$\overrightarrow{MN}$=(0,1,-2),$\overrightarrow{DP}$=(0,0,3),
设异面直线MN,PD所成角为θ,
则cosθ=|$\frac{\overrightarrow{MN}•\overrightarrow{DP}}{|\overrightarrow{MN}|•|\overrightarrow{DP}|}$|=|$\frac{-6}{\sqrt{5}×3}$|=$\frac{2\sqrt{5}}{5}$.
∴异面直线MN,PD所成角的余弦值为$\frac{2\sqrt{5}}{5}$.
点评 本题考查线面平行的证明,考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | {x|0<x<1} | B. | {x|x>1} | C. | {x|x≥2} | D. | {x|1<x<2} |
| A. | {a|a=4} | B. | {a|3≤a≤4} | C. | {a|3<a<4} | D. | Φ |
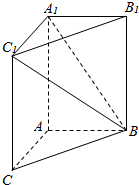 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.