Question

把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如下三角形数表：
    1
  3    5
7    9   11
…
…
设a_mn（m，n∈N^*）是位于这个三角形数表中从上往下数第m行、从左往右数第n个数．
（1）若a_mn=2011，求m，n的值；
（2）若记三角形数表中从上往下数第n行各数的和为b_n，求证+++…+．

Answer 1

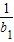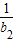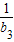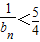【答案】分析：（1）由已知可得：三角形数表中前m行共有1+2+3+…+m=个数，于是第m行最后一个数应当是所给奇数列中的第项．故第m行最后一个数是=m²+m-1．  因此，使得a_mn=1011的m是不等式m²+m-1≥2011的最小正整数解．解出即可得到m．于是，第45行第一个数是44²+44-1+2=1981，再利用等差数列的通项公式即可得出m．
（2）由于第n行最后一个数是n²+n-1，且有n个数，所以若将n²+n-1看成第n行第一个数，则第n行各数成公差为-2的等差数列，故=n³．利用放缩法和裂项求和可得=，（n≥2）即可证明．
解答：解：（1）∵三角形数表中前m行共有1+2+3+…+m=个数，
∴第m行最后一个数应当是所给奇数列中的第项．
故第m行最后一个数是=m²+m-1．    
因此，使得a_mn=1011的m是不等式m²+m-1≥2011的最小正整数解．
化为m²+m-2012≥0，∴==44，
∴m=45．
于是，第45行第一个数是44²+44-1+2=1981，
∴n==16．
∴m=45，n=16．
（2）∵第n行最后一个数是n²+n-1，且有n个数，
若将n²+n-1看成第n行第一个数，则第n行各数成公差为-2的等差数列，
故=n³．
∴=，（n≥2）
∴+++…+
=1．
点评：熟练掌握等差数列的通项公式、前n项和公式、一元二次不等式的解法、放缩法、裂项求和等是解题的关键．