题目内容
试利用证明![]() ≥
≥![]() (a,b,c>0).
(a,b,c>0).
证法一:∵a,b,c>0,
∴a+b≥![]() ,c+
,c+![]() ≥2
≥2![]() ,
,
∴a+b+c+![]()
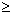
![]() +
+![]()
=![]() .
.
故a+b+c≥3·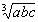 ,
,
即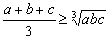 ,其中等号当且仅当a=b,c=
,其中等号当且仅当a=b,c=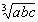 且
且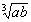 =
=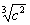 ,
,
即a=b=c时成立 .
证法二:设A=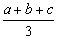 ,由a,b,c>0,得A>0,且a+b+c=3A,
,由a,b,c>0,得A>0,且a+b+c=3A,
于是A=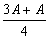
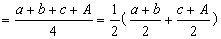
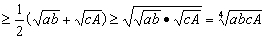
∴A4≥abcA,A≥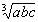 ,
,
即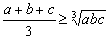 ,
,
等号当且仅当a=b,c=A,且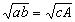 ,
,
即a=b=c时成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
试利用证明![]() ≥
≥![]() (a,b,c>0).
(a,b,c>0).
证法一:∵a,b,c>0,
∴a+b≥![]() ,c+
,c+![]() ≥2
≥2![]() ,
,
∴a+b+c+![]()
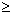
![]() +
+![]()
=![]() .
.
故a+b+c≥3·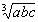 ,
,
即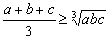 ,其中等号当且仅当a=b,c=
,其中等号当且仅当a=b,c=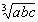 且
且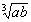 =
=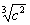 ,
,
即a=b=c时成立 .
证法二:设A=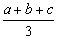 ,由a,b,c>0,得A>0,且a+b+c=3A,
,由a,b,c>0,得A>0,且a+b+c=3A,
于是A=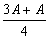
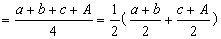
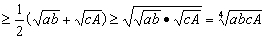
∴A4≥abcA,A≥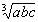 ,
,
即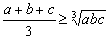 ,
,
等号当且仅当a=b,c=A,且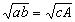 ,
,
即a=b=c时成立.

 阅读快车系列答案
阅读快车系列答案