题目内容
某某种饮料每箱6听,如果其中有两听不合格产品.
(1)质检人员从中随机抽出1听,检测出不合格的概率多大?;
(2)质检人员从中随机抽出2听,设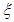 为检测出不合格产品的听数,求
为检测出不合格产品的听数,求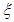 的分布列及数学期望.
的分布列及数学期望.
(1) ;(2)
;(2) =
= 。
。
解析试题分析:(1)在6听中随机抽出1听有6种方法 1分
在2听中随机抽出1听有2种方法 2分
所以 4分
4分
答: 5分
(1) 6分
6分
当 时,
时, 7分
7分
当 时,
时, 8分
8分
当 时,
时, 9分
9分
分布列为: 10分 11分
11分
= 12分
12分
考点:本题主要考查古典概型概率的计算,随机变量的分布列及数学期望。
点评:中档题,计算概率是关键,而明确“个数、方法数”更为关键,注意运用排列组合知识处理问题,不重不漏。

某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在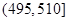 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.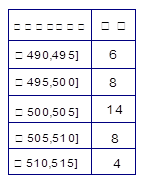
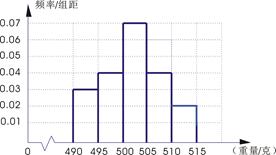
表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| | 甲流水线 | 乙流水线 | 合计 |
| 合格品 | 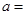 | 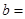 | |
| 不合格品 | 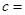 | 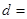 | |
| 合 计 | | |  |
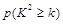 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
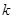 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
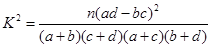 ,其中
,其中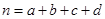 )
)
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素 ,
, 的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
 | 160 | 178 | 166 | 175 | 180 |
 | 75 | 80 | 77 | 70 | 81 |
(2)若
 且
且 为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数
为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数 的分布列及数学期望.
的分布列及数学期望. (8分)对某校高一年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
 | 25 |  |
 |  |  |
 | 2 | 0.05 |
| 合计 | M | 1 |

⑴求出表中
 、
、 及图中
及图中 的值;
的值;⑵若该校高一学生有720人,试估计他们参加社区服务的次数在区间
 内的人数;
内的人数;⑶在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
 内的概率.
内的概率. 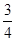 ,甲、丙二人都回答错的概率是
,甲、丙二人都回答错的概率是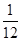 ,乙、丙二人都回答对的概率是
,乙、丙二人都回答对的概率是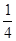 .
. ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。 ,求
,求
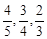 ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.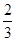 ,服用B有效的概率为
,服用B有效的概率为 。
。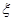 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求