题目内容
12.一个包装箱内有5件产品,其中3件正品,2件次品.现随机抽出两件产品检测,则事件“检测出次品”的概率为$\frac{7}{10}$.分析 把随机抽出两件产品恰好有次品这一事件列举出来,看方法数有多少,再列举总的方法数,两者相除即可.
解答 解:将5件产品编号,ABC(正品),d,e(次品),
从5件产品中选2件,其包含的基本事件为:
(AB)(AC)(Ad)(Ae),
(BC)(Bd)(Be)(Cd),
(Ce)(de)共有10种,
则“检测出次品”的概率为:p=$\frac{7}{10}$,
故答案为:$\frac{7}{10}$.
点评 在使用古典概型的概率公式时,应该注意:(1)要判断该概率模型是不是古典概型;(2)要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.

练习册系列答案
相关题目
3.下列关于条件语句的叙述,正确的是( )
| A. | 条件语句中必须有if、else和end | |
| B. | 条件语句中可以没有end | |
| C. | 条件语句中可以没有else,但必须有end | |
| D. | 条件语句中可以没有else及没end |
20.下列语句中的赋值语句是( )
| A. | x=x^3 | B. | 2=x | C. | x=y=2 | D. | x+y=z |
7.甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
(1)用茎叶图表示这两组数据;
(2)求两位学生预赛成绩的平均数和方差;
(3)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由.
| 甲 | 82 | 81 | 79 | 78 | 95 | 88 | 93 | 84 |
| 乙 | 92 | 95 | 80 | 75 | 83 | 80 | 90 | 85 |
(2)求两位学生预赛成绩的平均数和方差;
(3)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由.
17.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x^2}+{y^2}≤4\\ x-y≥0\end{array}$,则z=$\sqrt{{{(x+4)}^2}+{{(y-4)}^2}}$的最大值和最小值分别为( )
| A. | $36+16\sqrt{2}$,32 | B. | $4\sqrt{2}+2$,$4\sqrt{2}$ | C. | $36+16\sqrt{2}$,$4\sqrt{2}$ | D. | $36+16\sqrt{2}$,36 |
4.做一个容积为4升的正方形底无盖水箱,要使得材料最省,则此水箱底面边长为( )
| A. | $\frac{1}{2}$分米 | B. | 1分米 | C. | 2分米 | D. | 4分米 |
2.下列命题中正确的是( )
| A. | 若β=α+k•360°(k∈Z),则α与β终边相同 | B. | 第二象限角一定是钝角 | ||
| C. | 终边在y轴正半轴上的角是直角 | D. | 第四象限角一定是负角 |
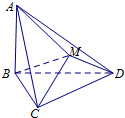 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,