题目内容
已知函数 (a为实常数).
(a为实常数).(Ⅰ)当a=1时,求函数g(x)=f(x)-2x的单调区间;
(Ⅱ)若函数f(x)在区间(0,2)上无极值,求a的取值范围;
(Ⅲ)已知n∈N*且n≥3,求证:
 .
.
【答案】分析:(Ⅰ)求出函数定义域,当a=1时求出g′(x),只需解不等式g′(x)>0,g′(x)<0即可.
(Ⅱ)函数f(x)在区间(0,2)上无极值,则f′(x)≥0或f′(x)≤0,由此即可求出a的取值范围.
(Ⅲ)由(Ⅱ)知,当a=1时,f(x)在(0,+∞)上的最大值为f(1)=0,得f(x)=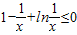 ≤0,即ln
≤0,即ln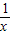
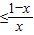 ,令x=
,令x= 适当变形即可证明.
适当变形即可证明.
解答:解:(I)当a=1时, ,其定义域为(0,+∞),g′(x)=-2+
,其定义域为(0,+∞),g′(x)=-2+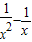 =
=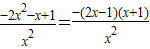 ,,
,,
令g′(x)>0,并结合定义域知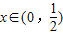 ; 令g′(x)<0,并结合定义域知
; 令g′(x)<0,并结合定义域知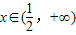 ;
;
故g(x)的单调增区间为(0, );单调减区间为
);单调减区间为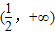 .
.
(II)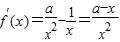 ,
,
(1)当f′(x)≤0即a≤x在x∈(0,2)上恒成立时,a≤0,此时f(x)在(0,2)上单调递减,无极值;
(2)当f′(x)≥0即a≥x在x∈(0,2)上恒成立时,a≥2,此时f(x)在(0,2)上单调递增,无极值.
综上所述,a的取值范围为(-∞,0]∪[2,+∞).
(Ⅲ)由(Ⅱ)知,当a=1时,f′(x)= ,当x∈(0,1)时,f′(x)>0,f(x)单调递增;
,当x∈(0,1)时,f′(x)>0,f(x)单调递增;
当x∈(1,+∞)时,f′(x)<0,f(x)单调递减,
∴f(x)=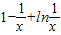 在x=1处取得最大值0.
在x=1处取得最大值0.
即f(x)=1-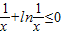 ,
,
∴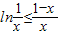 ,令x=
,令x=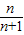 (0<x<1),则
(0<x<1),则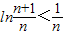 ,即ln(n+1)-lnn
,即ln(n+1)-lnn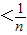 ,
,
∴ln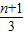 =ln(n+1)-ln3=[ln(n+1)-lnn]+[lnn-ln(n-1)]+…+(ln4-ln3)
=ln(n+1)-ln3=[ln(n+1)-lnn]+[lnn-ln(n-1)]+…+(ln4-ln3)
<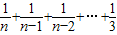 .
.
故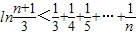 .
.
点评:本题考查了利用导数研究函数的单调性、利用导数求函数最值问题,考查了运用知识解决问题的能力.
(Ⅱ)函数f(x)在区间(0,2)上无极值,则f′(x)≥0或f′(x)≤0,由此即可求出a的取值范围.
(Ⅲ)由(Ⅱ)知,当a=1时,f(x)在(0,+∞)上的最大值为f(1)=0,得f(x)=
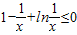 ≤0,即ln
≤0,即ln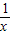
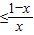 ,令x=
,令x= 适当变形即可证明.
适当变形即可证明.解答:解:(I)当a=1时,
 ,其定义域为(0,+∞),g′(x)=-2+
,其定义域为(0,+∞),g′(x)=-2+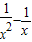 =
=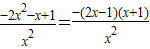 ,,
,,令g′(x)>0,并结合定义域知
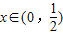 ; 令g′(x)<0,并结合定义域知
; 令g′(x)<0,并结合定义域知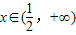 ;
;故g(x)的单调增区间为(0,
 );单调减区间为
);单调减区间为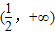 .
.(II)
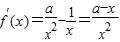 ,
,(1)当f′(x)≤0即a≤x在x∈(0,2)上恒成立时,a≤0,此时f(x)在(0,2)上单调递减,无极值;
(2)当f′(x)≥0即a≥x在x∈(0,2)上恒成立时,a≥2,此时f(x)在(0,2)上单调递增,无极值.
综上所述,a的取值范围为(-∞,0]∪[2,+∞).
(Ⅲ)由(Ⅱ)知,当a=1时,f′(x)=
 ,当x∈(0,1)时,f′(x)>0,f(x)单调递增;
,当x∈(0,1)时,f′(x)>0,f(x)单调递增;当x∈(1,+∞)时,f′(x)<0,f(x)单调递减,
∴f(x)=
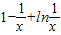 在x=1处取得最大值0.
在x=1处取得最大值0.即f(x)=1-
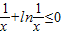 ,
,∴
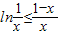 ,令x=
,令x=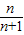 (0<x<1),则
(0<x<1),则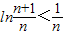 ,即ln(n+1)-lnn
,即ln(n+1)-lnn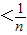 ,
,∴ln
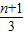 =ln(n+1)-ln3=[ln(n+1)-lnn]+[lnn-ln(n-1)]+…+(ln4-ln3)
=ln(n+1)-ln3=[ln(n+1)-lnn]+[lnn-ln(n-1)]+…+(ln4-ln3)<
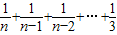 .
.故
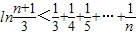 .
.点评:本题考查了利用导数研究函数的单调性、利用导数求函数最值问题,考查了运用知识解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a为实常数).
(a为实常数). 上有解,求实数a的取值范围;
上有解,求实数a的取值范围; ,它的前n项和为Sn,求证:
,它的前n项和为Sn,求证: .
. (a为实常数).
(a为实常数). 上有解,求实数a的取值范围;
上有解,求实数a的取值范围; ,它的前n项和为Sn,求证:
,它的前n项和为Sn,求证: .
. (a为实常数).
(a为实常数). .
. (a为实常数).
(a为实常数). .
.