题目内容
已知a=∫0π(sint-cost)dt,则(x-
)6的展开式中的常数项为( )
| 1 |
| ax |
| A、20 | ||
| B、-20 | ||
C、
| ||
D、-
|
分析:利用微积分基本定理求出a;利用二项展开式的通项公式求出展开式的通项,令x的指数为0,求出常数项.
解答:解:a=∫0π(sint-cost)dt=(-cost-sint)|0π=2,
∴(x-
)6=(x-
)6,
展开式的通项为Tr+1=(-
)r
x6-2r,
令6-2r=0得r=3,
所以展开式中的常数项为-
=-
,
故选D.
∴(x-
| 1 |
| ax |
| 1 |
| 2x |
展开式的通项为Tr+1=(-
| 1 |
| 2 |
| C | r 6 |
令6-2r=0得r=3,
所以展开式中的常数项为-
| 1 |
| 8 |
| C | 3 6 |
| 5 |
| 2 |
故选D.
点评:本题考查微积分基本定理、考查利用二项展开式的通项公式解决二项展开式的特定项问题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
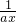 )6的展开式中的常数项为
)6的展开式中的常数项为