题目内容
已知函数![]() ,
,![]() .
.
(I)证明:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(II)对于给定的闭区间![]() ,试说明存在实数
,试说明存在实数 ![]() ,当
,当![]() 时,
时,![]() 在闭区间
在闭区间![]() 上是减函数;
上是减函数;
(III)证明:![]() .
.
本小题主要考查二次函数,利用导数研究函数的单调性和极值,函数的最大值和最小值等知识,考查综合运用数学知识解决问题的能力。
(Ⅰ)证明:由题设得![]()
又由![]() ,即
,即
![]()
由此可知,![]() 在R上为增函数。
在R上为增函数。
(Ⅱ)证法一:因为![]() 是
是![]() 为减函数的充分条件,所以只要找到实数k,使得t>k时,
为减函数的充分条件,所以只要找到实数k,使得t>k时,![]() ,即
,即![]()
在闭区间[![]() ]上成立即可
]上成立即可
因为![]() 在闭区间[
在闭区间[![]() ]上连续,故在闭区间[
]上连续,故在闭区间[![]() ]上有最大值,设其为k,于是在t>k时,
]上有最大值,设其为k,于是在t>k时,![]() 在闭区间[
在闭区间[![]() ]上恒成立,即
]上恒成立,即![]() 在闭区间[
在闭区间[![]() ]上为减函数。
]上为减函数。
证法二:因为![]() 是
是![]() 为减函数的充分条件,所以只要找到实数k,使得t>k时,
为减函数的充分条件,所以只要找到实数k,使得t>k时,![]() ,
,
在闭区间[![]() ]上成立即可。
]上成立即可。
令![]() ,则
,则![]() (
(![]() )当且仅当
)当且仅当
![]()
而上式成立只需
 即
即
成立取![]() 与
与![]() 中较大者记为k,易知当t>k时,
中较大者记为k,易知当t>k时,![]() 在闭区间[
在闭区间[![]() ]上恒成立,即
]上恒成立,即![]() 在闭区间[
在闭区间[![]() ]上为减函数
]上为减函数
(Ⅲ)证法一:设![]() ,即
,即
![]() ,
,
易得
![]()
令![]() ,则
,则![]() ,易知
,易知![]() ,当
,当![]() 时,
时,![]() >0,当
>0,当![]() 时,
时,![]() <0。故当
<0。故当![]() 时,
时,![]() 取得最小值,
取得最小值,![]() =1,所以
=1,所以
![]()
于是对任意![]() ,有
,有![]() ,即
,即![]()
证法二:设![]() ,
,
![]() 当且仅当
当且仅当
![]()
只需证明
![]() ,
,
即![]()
以下同证法一
证法三:设![]() ,则
,则
![]()
易得![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,故当
,故当![]()
![]() 时,
时,![]() 取得最小值
取得最小值![]() ,即
,即
![]()
![]()
![]()
以下同证法一
证法四:![]()
设点A、B的坐标分别为(![]() )、(t,t),易知点B在直线
)、(t,t),易知点B在直线![]() 上,令点A到直线
上,令点A到直线![]() 的距离为d,则
的距离为d,则
![]()
以下同证法一

练习册系列答案
相关题目
 ,
, .
. ,
, 。
。 的单调区间;
的单调区间; ,曲线C与其在点
,曲线C与其在点 处的切线交于另一点
处的切线交于另一点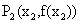 ,曲线C与其在点
,曲线C与其在点 ,线段
,线段
 (Ⅰ)(ii)的正确命题,并予以证明。
(Ⅰ)(ii)的正确命题,并予以证明。