题目内容
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥面BCD,∠ADB=60°,点E、F分别在AC、AD上,使面BEF⊥ACD,且EF∥CD,则平面BEF与平面BCD所成的二面角的正弦值为( )
分析:先判断∠EBC为平面BEF与平面BCD所成的二面角,再在△ABC中,求出平面BEF与平面BCD所成的二面角的正弦值.
解答:解:由题意,∵AB⊥面BCD,CD?面BCD,
∴AB⊥CD
∵∠BCD=90°
∴CD⊥BC
∵AB∩BC=B
∴CD⊥面ABC
∵BE?面ABC
∴CD⊥BE
∵EF∥CD
∴BE⊥EF
∵面BEF⊥面ACD,面BEF∩面ACD=EF
∴BE⊥面ACD
∵AC?面ACD
∴BE⊥AC
∵EF∥CD,EF?面BEF,EF?面BCD
∴EF∥面BCD
设面BEF∩面BCD=l
∴EF∥l
∴∠EBC为平面BEF与平面BCD所成的二面角
∵∠BCD=90°,BC=CD=1
∴BD=
∵AB⊥面BCD,∠ADB=60°
∴AB=
在△ABC中,BE⊥AC
∴∠EBC=∠BAC
∵AB=
,BC=1
∴AC=
∴sin∠BAC=
∴平面BEF与平面BCD所成的二面角的正弦值为
故选B.
∴AB⊥CD
∵∠BCD=90°
∴CD⊥BC
∵AB∩BC=B
∴CD⊥面ABC
∵BE?面ABC
∴CD⊥BE
∵EF∥CD
∴BE⊥EF
∵面BEF⊥面ACD,面BEF∩面ACD=EF
∴BE⊥面ACD
∵AC?面ACD
∴BE⊥AC
∵EF∥CD,EF?面BEF,EF?面BCD
∴EF∥面BCD
设面BEF∩面BCD=l
∴EF∥l
∴∠EBC为平面BEF与平面BCD所成的二面角

∵∠BCD=90°,BC=CD=1
∴BD=
| 2 |
∵AB⊥面BCD,∠ADB=60°
∴AB=
| 6 |
在△ABC中,BE⊥AC
∴∠EBC=∠BAC
∵AB=
| 6 |
∴AC=
| 7 |
∴sin∠BAC=
| ||
| 7 |
∴平面BEF与平面BCD所成的二面角的正弦值为
| ||
| 7 |
故选B.
点评:本题是求无棱二面角的平面角,解题的关键是正确作出二面角的平面角,难度较大,很容易做错,要小心.

练习册系列答案
相关题目
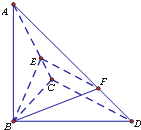 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且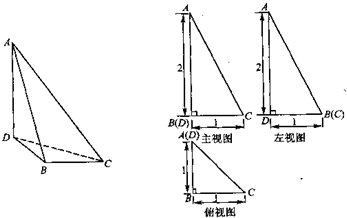 (2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.
(2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.