题目内容
已知曲线C1:![]() (
(![]() 为参数),曲线C2:
为参数),曲线C2: (t为参数).
(t为参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线![]() .写出
.写出![]() 的参数方程.
的参数方程. ![]() 与
与![]() 公共点的个数和C
公共点的个数和C![]() 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
解:(Ⅰ)C1是圆,C2是直线,
C1的普通方程为![]() ,圆心
,圆心![]() ,半径r=1。
,半径r=1。
C2的普通方程为![]() 。
。
因为圆心C1到直线![]() 的距离为1,
的距离为1,
所以C2与C1只有一个公共点。
(Ⅱ)压缩后的参数方程分别为
 (
(![]() 为参数),
为参数), (
(![]() 为参数)。
为参数)。
化为普通方程为![]() ,
,![]() ,
,
联立消元,得![]() ,
,
其判别式![]() ,
,
所以压缩后的直线![]() 与椭圆
与椭圆![]() 仍然只有一个公共点,和C2与C1公共点个数相同。
仍然只有一个公共点,和C2与C1公共点个数相同。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
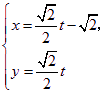 (t为参数).
(t为参数).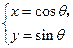 (
(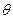 为参数),曲线C2:
为参数),曲线C2: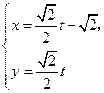 (t为参数).
(t为参数).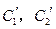 .写出
.写出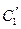 与
与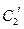 公共点的个数和C
公共点的个数和C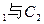 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.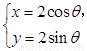 (
(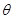 为参数),曲线C2:
为参数),曲线C2: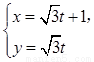 (t为参数).
(t为参数).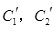 .写出
.写出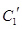 与
与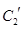 公共点的个数和C
公共点的个数和C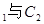 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.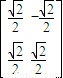 对应的变换作用下得到的曲线C′的方程.
对应的变换作用下得到的曲线C′的方程.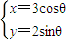 (θ为参数)和曲线C2:ρsin(θ-
(θ为参数)和曲线C2:ρsin(θ-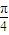 )=
)=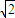 .
.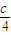 ,|y-b|<
,|y-b|<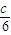 ,求证:|2x-3y-2a+3b|<c.
,求证:|2x-3y-2a+3b|<c.
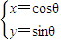 (θ为参数),曲线C2:
(θ为参数),曲线C2: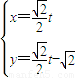 (t为参数),
(t为参数),