题目内容
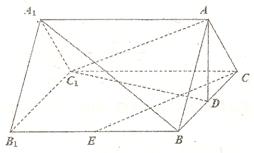
如图,在直三棱柱ABC-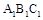 中,
中,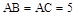 ,D,E分别为BC,
,D,E分别为BC,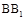 的中点,
的中点,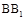 的中点,四边形
的中点,四边形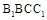 是边长为6的正方形.
是边长为6的正方形.
(1)求证: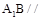 平面
平面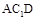 ;
;
(2)求证: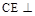 平面
平面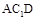 ;
;
(3)求二面角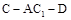 的余弦值.
的余弦值.
【答案】
(1)证明:连结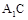 ,与
,与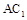 交于O点,连结OD.
交于O点,连结OD.
因为O,D分别为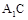 和BC的中点,
和BC的中点,
所以OD//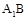 。
。
又OD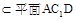 ,
, 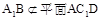 ,
,
所以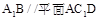 .…………………………4分
.…………………………4分
(2)证明:在直三棱柱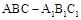 中,
中,
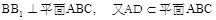 ,
,
所以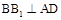 .
.
因为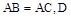 为BC中点,
为BC中点,
所以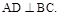 又
又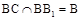 ,
,
所以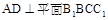 .
.
又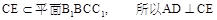
因为四边形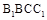 为正方形,D,E分别为BC,
为正方形,D,E分别为BC,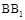 的中点,
的中点,
所以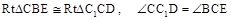 .
.
所以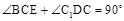 . 所以
. 所以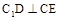
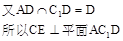
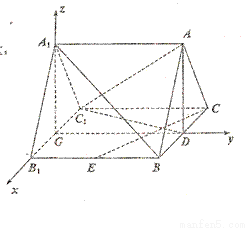
(3)解:如图,以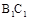 的中点G为原点,建立空间直角坐标系,
的中点G为原点,建立空间直角坐标系,
则A(0,6,4),E(3,3,0) ,C(-3,6,0) ,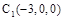 .
.
由(Ⅱ)知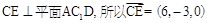 为平面
为平面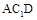 的一个法向量。
的一个法向量。
设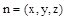 为平面
为平面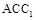 的一个法向量,
的一个法向量,
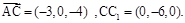
由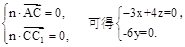
令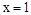 ,则
,则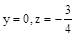 .
.
所以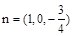 .
.
从而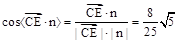 .
.
因为二面角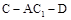 为锐角,
为锐角,
所以二面角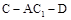 的余弦值为
的余弦值为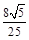
【解析】略

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目




