题目内容
设a>0,且a≠1,函数y=ax2-2x+3有最大值,求函数f(x)=loga(3-2x)的单调区间.
解:设t=x2-2x+3=(x-1)2+2.
当x∈R时,t有最小值,为2.
∵y=ax2-2x+3有最大值,∴0<a<1.
由f(x)=loga(3-2x),得其定义域为(-∞,![]() ).
).
设u(x)=3-2x,x∈(-∞,![]() ),则f(x)=logau(x).
),则f(x)=logau(x).
∵u(x)=3-2x在(-∞,![]() )上是减函数,0<a<1,
)上是减函数,0<a<1,
∴f(x)=logau(x)在(-∞,![]() )上是增函数.
)上是增函数.
∴f(x)=loga(3-2x)的单调增区间为(-∞,![]() ),无单调减区间.
),无单调减区间.

练习册系列答案
相关题目
 ”索的因应是( )
”索的因应是( )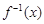 .
.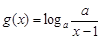 ,求不等式g(x)≤
,求不等式g(x)≤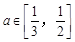 恒成立的x的取值范围.
恒成立的x的取值范围.