题目内容
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y= ![]() 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 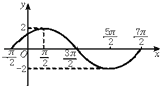
【答案】f(x)=2sin( ![]() x+
x+ ![]() );(
);( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z)
)(k∈Z)
【解析】解:∵f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R),
∴A=2,周期T= ![]() =
= ![]() ﹣(﹣
﹣(﹣ ![]() )=4π,
)=4π,
∴ω= ![]() .
.
∴f(x)=2sin( ![]() x+φ),
x+φ),
又f(﹣ ![]() )=2sin(
)=2sin( ![]() ×(﹣
×(﹣ ![]() )+φ)=0,
)+φ)=0,
∴φ﹣ ![]() =kπ,k∈Z,|φ|<π,
=kπ,k∈Z,|φ|<π,
∴φ= ![]() .
.
∴f(x)=2sin( ![]() x+
x+ ![]() ).
).
当f(x)= ![]() 时,即2sin(
时,即2sin( ![]() x+
x+ ![]() )=
)= ![]() ,可得sin(
,可得sin( ![]() x+
x+ ![]() )=
)= ![]() ,
,
∴ ![]() x+
x+ ![]() =
= ![]() +2kπ或
+2kπ或 ![]() x+
x+ ![]() =
= ![]() +2kπ(k∈Z),可得x=
+2kπ(k∈Z),可得x= ![]() +4kπ或
+4kπ或 ![]() +4kπ(k∈Z)
+4kπ(k∈Z)
由此可得,直线y= ![]() 与函数f(x)图象的所有交点的坐标为:(
与函数f(x)图象的所有交点的坐标为:( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z).
)(k∈Z).
所以答案是:f(x)=2sin( ![]() x+
x+ ![]() ),(
),( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z).
)(k∈Z).

练习册系列答案
相关题目