题目内容
已知函数y=（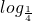
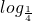x）2-x+5，x∈[2，4]，f（x）最大值为 ________．
7
分析：先用换元法对原函数转化，转化为求f（t）=t2-t+5，t∈[-1，
]上的最大值，在利用开口向上的二次函数离对称轴越远函数值越大来求即可．
解答：令log
x=t，∵x∈[2，4]，∴t∈[-1，-]
转化为求f（t）=t2-t+5在t∈[-1，-]上的最大值．
∵f（t）=t2-t+5 开口向上 对称轴为 t=
∴f（t）=t2-t+5在t∈[-1，-]上的最大值为f（-1）=7
故答案为 7．
点评：本题的实质是求二次函数的最值问题，关于给定解析式的二次函数在固定闭区间上的最值问题，一般是根据对称轴和闭区间的位置关系来进行分类讨论，如轴在区间左边，轴在区间右边，轴在区间中间，最后在综合归纳得出所需结论．
分析：先用换元法对原函数转化，转化为求f（t）=t2-t+5，t∈[-1，
]上的最大值，在利用开口向上的二次函数离对称轴越远函数值越大来求即可．解答：令log
x=t，∵x∈[2，4]，∴t∈[-1，-]转化为求f（t）=t2-t+5在t∈[-1，-
]上的最大值．∵f（t）=t2-t+5 开口向上 对称轴为 t=
∴f（t）=t2-t+5在t∈[-1，-
]上的最大值为f（-1）=7故答案为 7．
点评：本题的实质是求二次函数的最值问题，关于给定解析式的二次函数在固定闭区间上的最值问题，一般是根据对称轴和闭区间的位置关系来进行分类讨论，如轴在区间左边，轴在区间右边，轴在区间中间，最后在综合归纳得出所需结论．
练习册系列答案
名校课堂系列答案
相关题目
已知函数y=tanωx在(-
，
)上是减函数，则（ ）
| π |
| 2 |
| π |
| 2 |
| A、0＜ω≤1 | B、-1≤ω＜0 |
| C、ω≥1 | D、ω≤-1 |
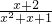（x＞-2）
的取值范围；