题目内容
【题目】已知单调递增的等比数列![]() 满足
满足![]() ,且
,且![]() 是
是![]() ,
, ![]() 的等差中项.
的等差中项.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() (
(![]() )是单调递增数列?若存在,求出
)是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)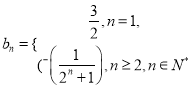 ; (Ⅲ)
; (Ⅲ)![]() .
.
【解析】试题分析:
(Ⅰ)由题意求得![]() ,
, ![]() ,∴
,∴![]() ;
;
(Ⅱ)利用题意错位相减可得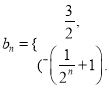
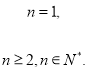 ;
;
(Ⅲ)题中不等式转化为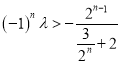 ,分类讨论当
,分类讨论当![]() 为大于或等于4的偶数,当
为大于或等于4的偶数,当![]() 为大于或等于3的奇数时,两种情况可得
为大于或等于3的奇数时,两种情况可得![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)设此等比数列为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,其中
,…,其中![]() ,
, ![]() .
.
由题意知: ![]() ,①
,①
![]() .②
.②
②![]() ①得
①得![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() .
.
∵等比数列![]() 单调递增,∴
单调递增,∴![]() ,
, ![]() ,∴
,∴![]() ;
;
(Ⅱ)由(Ⅰ)可知![]() (
(![]() ),
),
由![]() (
(![]() ),
),
得![]() (
(![]() ),
),
故![]() ,即
,即![]() (
(![]() ),
),
当![]() 时,
时, ![]() ,
, ![]() ,∴
,∴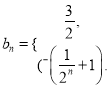
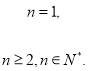 ;
;
(Ⅲ)∵![]() ,
,
∴当![]() 时,
时, ![]() ,
, ![]() ,
,
依据题意,有![]() ,
,
即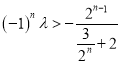 ,
,
①当![]() 为大于或等于4的偶数时,有
为大于或等于4的偶数时,有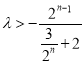 恒成立,
恒成立,
又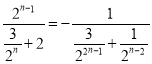 随
随![]() 增大而增大,
增大而增大,
则当且仅当![]() 时,
时, 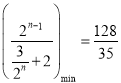 ,故
,故![]() 的取值范围为
的取值范围为![]() ;
;
②当![]() 为大于或等于3的奇数时,有
为大于或等于3的奇数时,有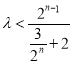 恒成立,且仅当
恒成立,且仅当![]() 时,
时, 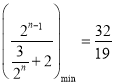 ,故
,故![]() 的取值范围为
的取值范围为![]() ;
;
又当![]() 时,由
时,由![]() ,得
,得![]() ,
,
综上可得,所求![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目