题目内容
3.某校高二年级的仪仗队由6名男生和6名女生组成.(1)某次活动需要从仪仗队中选出4名男生和3名女生站成一排,且女生相邻,那么排列方法有多少种?
(2)仪仗队中有3个男生和2个女生参加一次训练,教官随机地从中选出一人,若选出的是男生,则对他进行10分钟正步训练,若选出的是女生,则对她进行5分钟正步训练.完成训练的学生不再归队,教官再随机地选出另外一人,直到完成训练的男生多于女生为止,整个训练结束.设本次训练的总时间为ξ,求ξ的分布列与期望.
分析 (1)先选3名女生并捆绑在一起,再和选出的4名男生全排列,问题得以解决,
(2)由题意可知,则ξ可以为10分钟(一名男生),25分钟(2名男生和1名女生),40分钟(5人全部参加),得到分布列,根据数学期望公式得到答案.
解答 解:(1)先选3名女生并捆绑在一起,再和选出的4名男生全排列,故有A63C64A55=216000种,
(2)设本次训练的总时间为ξ,则ξ可以为10分钟,25分钟,40分钟,
P(ξ=10)=$\frac{3}{5}$
P(ξ=25)=$\frac{1}{5}$,
P(ξ=40)=$\frac{1}{5}$,
则ξ的分布列为:
| ξ | 10 | 25 | 40 |
| P | $\frac{3}{5}$ | $\frac{1}{5}$ | $\frac{1}{5}$ |
点评 本题考查了排列组合和分布列数学期望的问题,属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
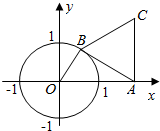 如图的平面直角坐标系中,O为坐标原点,点B在单位圆上,A(2,0),∠AOB=θ,△ABC为等边三角形.
如图的平面直角坐标系中,O为坐标原点,点B在单位圆上,A(2,0),∠AOB=θ,△ABC为等边三角形.