题目内容
18.已知f(x)=$\left\{\begin{array}{l}{\frac{x}{{x}^{2}+1},x≥0}\\{-\frac{1}{x},x<0}\end{array}\right.$,若函数g(x)=f(x)-t有三个不同的零点x1,x2,x3(x1<x2<x3),则-$\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}$的取值范围是$(\frac{5}{2},+∞)$.
分析 画出函数的图象,求出x≥0时f(x)的最大值,判断零点的范围,然后推出结果.
解答 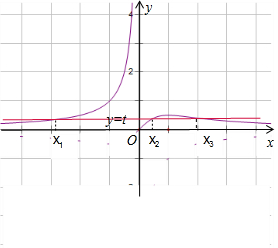 解:函数f(x)=$\left\{\begin{array}{l}{\frac{x}{{x}^{2}+1},x≥0}\\{-\frac{1}{x},x<0}\end{array}\right.$,图象如图,
解:函数f(x)=$\left\{\begin{array}{l}{\frac{x}{{x}^{2}+1},x≥0}\\{-\frac{1}{x},x<0}\end{array}\right.$,图象如图,
函数g(x)=f(x)-t有三个不同的零点x1,x2,x3,
且x1<x2<x3,即方程f(x)=t有三个不同的实数根
x1,x2,x3,且x1<x2<x3,
当x>0时,f(x)=$\frac{1}{x+\frac{1}{x}}$,因为x+$\frac{1}{x}$≥2(x>0),
所以f(x)$≤\frac{1}{2}$,当且仅当x=1时取得最大值.
当y=$\frac{1}{2}$时,x1=-2;x2=x3=1,
此时-$\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}$=$\frac{5}{2}$,
由$\frac{1}{x+\frac{1}{x}}$=t(0$<t<\frac{1}{2}$),可得${x}^{2}-\frac{x}{t}+1$=0,∴x2+x3=$\frac{1}{t}$,x2x3=1
∴$\frac{1}{{x}_{2}}$+$\frac{1}{{x}_{3}}$=$\frac{1}{t}$>2,
∴-$\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}$=t+$\frac{1}{t}$
∵0$<t<\frac{1}{2}$,∴-$\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}$的取值范围是$(\frac{5}{2},+∞)$.
故答案为$(\frac{5}{2},+∞)$.
点评 本题考查函数的零点个数的判断与应用,基本不等式的应用,考查数形结合思想以及转化思想的应用.

| A. | 36π | B. | 16π | C. | $\frac{9π}{2}$ | D. | $\frac{9π}{4}$ |
| A. | 21 | B. | 35 | C. | 63 | D. | 126 |
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
| A. | 3 | B. | 2或3 | C. | 2 | D. | 6 |