题目内容
设平面内有△ABC及点O，若满足关系式：
，那么△ABC一定是（ ）A．直角三角形
B．等腰直角三角形
C．等腰三角形
D．等边三角形
【答案】分析：利用两个向量的加减法的法则可得（
）•[（
）+（
）]=0，即（
）•[
]=0，得到|AB|=|AC|．
解答：解：∵
，
∴（
）•[（
）+（
）]=0，
∴（
）•[
]=0，
=
，
∴|AB|=|AC|，
故△ABC一定是等腰三角形，
故选C．
点评：本题考查两个向量的加减法的法则，以及其几何意义，向量的模的定义，求向量的模的方法，得到
（
）•[（
）+（
）]=0，是解题的难点．
）•[（ ）+（）]=0，即（ ）•[]=0，得到|AB|=|AC|．解答：解：∵
，∴（
）•[（ ）+（）]=0，∴（
）•[]=0，=，∴|AB|=|AC|，
故△ABC一定是等腰三角形，
故选C．
点评：本题考查两个向量的加减法的法则，以及其几何意义，向量的模的定义，求向量的模的方法，得到
（
）•[（ ）+（）]=0，是解题的难点． 
练习册系列答案
相关题目
设平面内有△ABC及点O，若满足关系式：(
-
)•(
+
-2
) = 0，那么△ABC一定是（ ）
| OB |
| OC |
| OB |
| OC |
| OA |
| A、直角三角形 |
| B、等腰直角三角形 |
| C、等腰三角形 |
| D、等边三角形 |
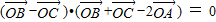，那么△ABC一定是（ ）
，那么△ABC一定是（ ）