题目内容
已知函数
(1)求 的单调区间和极值;
的单调区间和极值;
(2)若对于任意的 ,都存在
,都存在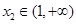 ,使得
,使得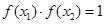 ,求
,求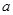 的取值范围
的取值范围
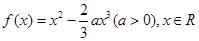
(1)求
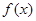 的单调区间和极值;
的单调区间和极值;(2)若对于任意的
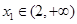 ,都存在
,都存在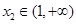 ,使得
,使得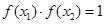 ,求
,求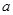 的取值范围
的取值范围(1) 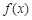 的单调增区间是
的单调增区间是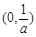 ,单调减区间是
,单调减区间是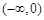 和
和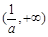 ,当
,当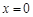 时,
时,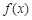 取极小值
取极小值 ,当
,当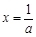 时,
时,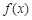 取极大值
取极大值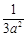 , (2)
, (2) 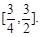
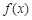 的单调增区间是
的单调增区间是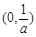 ,单调减区间是
,单调减区间是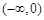 和
和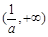 ,当
,当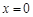 时,
时,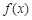 取极小值
取极小值 ,当
,当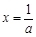 时,
时,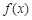 取极大值
取极大值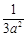 , (2)
, (2) 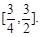
试题分析:(1)求函数单调区间及极值,先明确定义域:R,再求导数
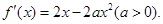 在定义域下求导函数的零点:
在定义域下求导函数的零点: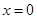 或
或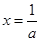 ,通过列表分析,根据导函数符号变化规律,确定单调区间及极值,即
,通过列表分析,根据导函数符号变化规律,确定单调区间及极值,即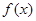 的单调增区间是
的单调增区间是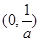 ,单调减区间是
,单调减区间是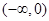 和
和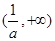 ,当
,当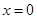 时,
时,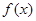 取极小值
取极小值 ,当
,当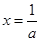 时,
时,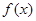 取极大值
取极大值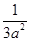 , (2)本题首先要正确转化:“对于任意的
, (2)本题首先要正确转化:“对于任意的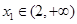 ,都存在
,都存在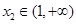 ,使得
,使得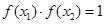 ”等价于两个函数值域的包含关系.设集合
”等价于两个函数值域的包含关系.设集合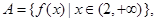 ,集合
,集合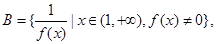 则
则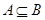 ,其次挖掘隐含条件,简化讨论情况,明确讨论方向.由于
,其次挖掘隐含条件,简化讨论情况,明确讨论方向.由于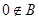 ,所以
,所以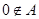 ,因此
,因此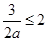 ,又
,又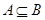 ,所以
,所以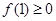 ,即
,即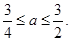
解(1)由已知有
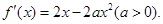 令
令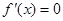 ,解得
,解得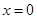 或
或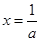 ,列表如下:
,列表如下: |  |  |  |  | 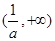 |
 | 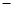 |  |  |  | 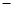 |
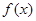 |  |  |  | 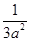 |  |
 的单调增区间是
的单调增区间是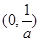 ,单调减区间是
,单调减区间是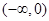 和
和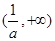 ,当
,当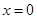 时,
时,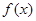 取极小值
取极小值 ,当
,当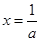 时,
时,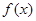 取极大值
取极大值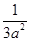 ,(2)由
,(2)由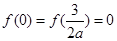 及(1)知,当
及(1)知,当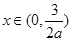 时,
时,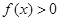 ,当
,当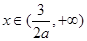 时,
时,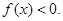 设集合
设集合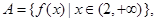 ,集合
,集合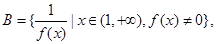 则“对于任意的
则“对于任意的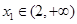 ,都存在
,都存在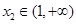 ,使得
,使得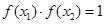 ”等价于
”等价于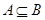 .显然
.显然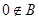 .
.下面分三种情况讨论:
当
 即
即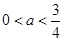 时,由
时,由 可知
可知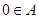 而
而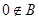 ,所以A不是B的子集
,所以A不是B的子集当
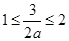 即
即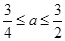 时,有
时,有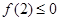 且此时
且此时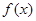 在
在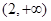 上单调递减,故
上单调递减,故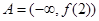 ,因而
,因而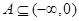 由
由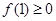 有
有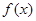 在
在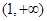 上的取值范围包含
上的取值范围包含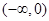 ,所以
,所以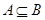
当
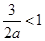 即
即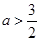 时,有
时,有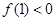 且此时
且此时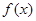 在
在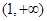 上单调递减,故
上单调递减,故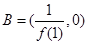 ,
,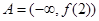 ,所以A不是B的子集
,所以A不是B的子集综上,
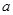 的取值范围为
的取值范围为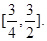

练习册系列答案
相关题目
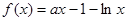 (
(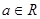 )
)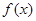 的单调性;
的单调性;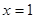 处取得极值,不等式
处取得极值,不等式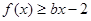 对任意
对任意 恒成立,求实数
恒成立,求实数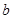 的取值范围;
的取值范围;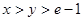 时,证明不等式
时,证明不等式 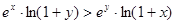 .
.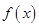 =
=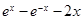 .
.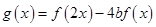 ,当
,当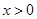 时,
时,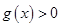 ,求
,求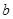 的最大值;
的最大值;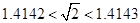 ,估计ln2的近似值(精确到0.001)
,估计ln2的近似值(精确到0.001) 在
在 时取得极小值.
时取得极小值. 的值;
的值; ,使得
,使得 在该区间上的值域为
在该区间上的值域为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. ,若
,若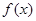 存在唯一的零点
存在唯一的零点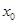 ,且
,且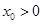 ,则
,则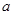 的取值范围是
的取值范围是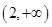

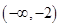
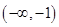
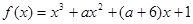 有极大值和极小值,则
有极大值和极小值,则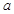 的取值范围为( )
的取值范围为( )
 2
2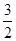 )
)