题目内容
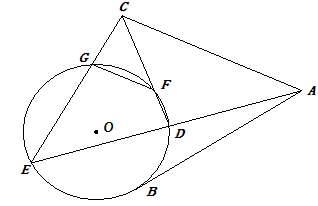
 如图,
如图, |
| AC |
 |
| AC |
 |
| AC |
(1)若∠B=75°,则∠ADC=
110°
110°
;(2)若⊙O的半径长为
| 5 |
| 2 |
| 25 |
| 13 |
| 25 |
| 13 |
分析:(1)设∠A=α,由题意可得,∠ADC=∠B+∠BCD=75°+∠BCD,∠A=∠BCD=∠ACD,结合三角形的 内角和定理即可求解α,进而可求∠ADC
(2)由题意可得,∠ACD=∠CAD=∠BCD=α,由正弦定理可得,
=2r=5可求sinα,然后再次利用正弦定理可得BC与BD的关系,由切割线定理可得,BC2=BD•BA可求
(2)由题意可得,∠ACD=∠CAD=∠BCD=α,由正弦定理可得,
| 3 |
| sinα |
解答:解:(1)设∠A=α
由题意可得,∠ADC=∠B+∠BCD=75°+∠BCD
∵BC切
于点C,CD平分∠ACB
由弦切角定理可得,∠A=∠BCD=∠ACD
∵∠A+∠BDC+∠BCD=180°
∴75°+α+α+α=180°
∴α=35°
∴∠ADC=75°+α=110°
(2)由题意可得,∠ACD=∠CAD=∠BCD=α
∵△ADC为圆的内接三角形
由正弦定理可得,
=2r=5
∴sinα=
,cosα=
△BCD中,∠CDB=2α
由正弦定理可得,
=
∴
=
=2cosα=
由切割线定理可得,BC2=BD•BA
即
BD2=BD•(BD+3)
∴BD=
故答案为:110°,
由题意可得,∠ADC=∠B+∠BCD=75°+∠BCD
∵BC切
 |
| AC |
由弦切角定理可得,∠A=∠BCD=∠ACD
∵∠A+∠BDC+∠BCD=180°
∴75°+α+α+α=180°
∴α=35°
∴∠ADC=75°+α=110°
(2)由题意可得,∠ACD=∠CAD=∠BCD=α
∵△ADC为圆的内接三角形
由正弦定理可得,
| 3 |
| sinα |
∴sinα=
| 3 |
| 5 |
| 4 |
| 5 |
△BCD中,∠CDB=2α
由正弦定理可得,
| BD |
| sin2α |
| BC |
| sinα |
∴
| BC |
| BD |
| sin2α |
| sinα |
| 8 |
| 5 |
由切割线定理可得,BC2=BD•BA
即
| 64 |
| 25 |
∴BD=
| 25 |
| 13 |
故答案为:110°,
| 25 |
| 13 |
点评:本题主要考查了圆的圆周角定理、切割线定理等知识的综合应用,解答本题的关键是灵活利用了正弦定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
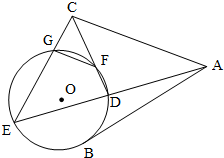 如图,AB是⊙O的一条切线,切点为B,ADE,CFD,CGE都是⊙O的割线,已知AC=AB.
如图,AB是⊙O的一条切线,切点为B,ADE,CFD,CGE都是⊙O的割线,已知AC=AB. 选修4-1:几何证明选讲.
选修4-1:几何证明选讲.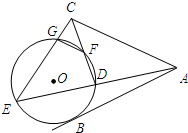 (2013•徐州一模)选修4-1:几何证明选讲
(2013•徐州一模)选修4-1:几何证明选讲