题目内容
如图，AB是⊙O的一条切线，切点为B，ADE，CFD，CGE都是⊙O的割线，已知AC=AB。
（1）证明：AD·AE=AC2；
（2）证明：FG∥AC。
（1）证明：AD·AE=AC2；
（2）证明：FG∥AC。
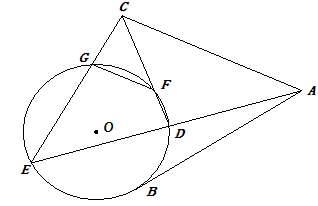
| 证明：（1）∵AB是⊙O的一条切线，AE为割线， ∴AB2=AD·AE， 又∵AB=AC， ∴AD·AE=AC2； （2）由（1）有  ，∵∠EAC=∠DAC， ∴△ADC∽△ACE， ∴∠ADC=∠ACE， ∵∠ADC=∠EGF， ∴∠EGF=∠ACE， ∴GF∥AC。 |
 |
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
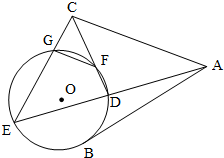如图，AB是⊙O的一条切线，切点为B，ADE，CFD，CGE都是⊙O的割线，已知AC=AB．
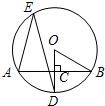如图，AB是⊙O的一条弦，OD⊥AB于点C，交⊙O于点D，点E在⊙O上，∠AED=25°，则∠OBA的度数是
选修4-1：几何证明选讲．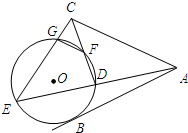
（2013•徐州一模）选修4-1：几何证明选讲
选修4-1：几何证明选讲