题目内容
若α同时满足tanα<0,cosα>0,(1)求α的集合;
(2)判断sin![]() ,cos
,cos![]() ,tan
,tan![]() 的符号.
的符号.
解:(1)由cosα>0知α的终边在第一或第四象限,或在x轴的非负半轴上.由tanα<0,得α终边又在第二、四象限.因此,α的终边在第四象限.
∴角α的集合为{α|2kπ-![]() <α<2kπ,k∈Z }.
<α<2kπ,k∈Z }.
(2)∵2kπ-![]() <α<2kπ,k∈Z,
<α<2kπ,k∈Z,
∴kπ-![]() <
<![]() <kπ,k∈Z.
<kπ,k∈Z.
当k=2n(n∈Z)时,2nπ-![]() <
<![]() <2nπ.
<2nπ.
∴sin![]() <0,cos
<0,cos![]() >0,tan
>0,tan![]() <0;
<0;
当k=2n+1(n∈Z)时,2nπ+![]() <
<![]() <2nπ+π.
<2nπ+π.
∴sin![]() >0,cos
>0,cos![]() <0,tan
<0,tan![]() <0.
<0.
温馨提示
(1)要熟记三角函数值在各象限的符号.
(2)α为象限角,求![]() 是哪个象限角的方法:根据α所在象限写出α的不等式,进而得
是哪个象限角的方法:根据α所在象限写出α的不等式,进而得![]() 的不等式.再对k为奇数、偶数两种情况讨论.
的不等式.再对k为奇数、偶数两种情况讨论.

练习册系列答案
相关题目
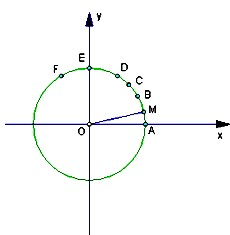 如图,圆O为单位圆,A(1,0),
如图,圆O为单位圆,A(1,0),