Question

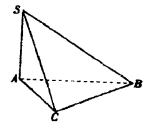
如下图，在三棱锥S－ABC中，∠SAB＝∠SAC＝∠ACB＝90°，AC＝2，，．

（Ⅰ）证明：SC⊥BC；

（Ⅱ）求侧面SBC与底面ABC所成二面角的大小；

（Ⅲ）求异面直线SC与AB所成的角的大小（用反三角函数表示）．

Answer 1

答案：
解析：

解：（Ⅰ）∵  ，  ∴  ，  ，  ∴  ． 　　由于，即，  由三垂线定理，得  ； （Ⅱ）∵  ，，  ∴  是侧面与底面所成二面角的平面角． 　　在△中，由，，得  ． 　　在△中，由，，得  ． 　　∴  ．  即  侧面与底面所成二面角的大小为． 　　（Ⅲ）如下图，过点作，过点作的平行线交于，连结，则是异面直线与所成的角．又四边形是平行四边形， 　　，  ， 　　． 　　在△中，  ， 　　∴  与所成的角的大小为．