题目内容

已知圆O的半径为1，半径OA、OB的夹角为θ（0＜θ＜π），θ为常数，点C为圆O上的动点，若 $数学公式$ ，则x+y的最大值为________．

$\text{[math]}$
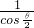
分析：利用向量的模的运算性质与向量的数量积可求得x+y与θ的关系式，利用基本不等式与三角函数的升幂公式及可求得答案．
解答：∵圆O的半径为1，半径OA、OB的夹角为θ（0＜θ＜π），点C为圆O上的动点， $\text{[math]}$ =x $\text{[math]}$ +y $\text{[math]}$ （x，y∈R），
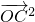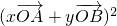∴ $\text{[math]}$ = $\text{[math]}$ =x²+2xycosθ+y²=1，
∴（x+y）²-2xy+2xycosθ=1，
∴2xy（1-cosθ）=（x+y）²-1，
∵0＜θ＜π，
∴1-cosθ≠0，
∴2xy= 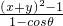$\text{[math]}$ ，不妨令x＞0，y＞0，
则2xy= 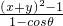$\text{[math]}$ ≤2× $\text{[math]}$ ，令t=x+y（x＞0，y＞0），
则t²-1≤ $\text{[math]}$ t²（1-cosθ），
整理得：t²≤ $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
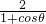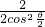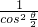∴0＜t≤ $\text{[math]}$ ．
即x+y≤ $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题考查向量的模的运算性质与向量的数量积，着重考查基本不等式与三角函数的升幂公式的应用，考查换元思想与化归思想，属于难题．