Question

【题目】设．

（1）求的单调区间；

（2）在锐角中，角的对边分别为若， ，求面积的最大值．

Answer 1

【答案】（1）增区间，减区间为；（2）

【解析】试题分析：（1）将函数化为，然后根据正弦函数的单调区间求解；

（2）由求得，然后根据余弦定理得到，由基本不等式可得，进而可得三角形面积的最大值。

试题解析：

(1)由题意知，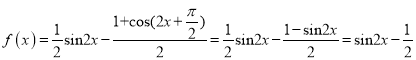

由－＋2kπ≤2x≤＋2kπ，k∈Z，

可得－＋kπ≤x≤＋kπ，k∈Z；

由＋2kπ≤2x≤＋2kπ，k∈Z，

可得＋kπ≤x≤＋kπ，k∈Z.

所以f(x)的单调递增区间是[－＋kπ， ＋kπ](k∈Z)；单调递减区间是[＋kπ， ＋kπ](k∈Z)．

(2)由f()＝sinA－＝0，得sinA＝，

由题意知A为锐角，

所以cosA＝，

由余弦定理得，

所以，当且仅当b＝c时等号成立，

所以，

所以

所以△ABC面积的最大值为。