题目内容
如图,在四棱柱![]() 中,底面
中,底面![]() 是正方形,侧棱与底面垂直,点
是正方形,侧棱与底面垂直,点![]() 是正方形
是正方形![]() 对角线的交点,
对角线的交点,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 和
和![]() 上,且
上,且![]() .
.
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角![]() 的余弦值.
的余弦值.

解:(Ⅰ)证明:取![]() ,连结
,连结![]() 和
和![]() ,
,

∴![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ∥
∥![]() ,
,
∴![]() ,
,![]() ∥
∥![]() .
.
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ∥
∥![]() ,
,
在矩形![]() 中,
中,![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.
∴![]() ∥
∥![]() ,
,![]() ∥
∥![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() . ————————4分
. ————————4分
(Ⅱ)连结![]() ,在正四棱柱
,在正四棱柱![]() 中,
中,
![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
由已知![]() ,得
,得![]() 平面
平面![]() .
.
∴![]() ,
,![]() ,
,
在△![]()
![]() 与△
与△![]() 中,
中, ![]() ,
,![]() ,
,
∴△![]() ∽△
∽△![]()
∴![]() ,
,![]() .—————————9分
.—————————9分
(Ⅲ)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.

![]() .
.
![]() ,
,
由(Ⅱ)知![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则  ,即
,即  ,
,
令![]() ,所以
,所以 ![]() .
.
∴![]() ,
,
∵二面角![]() 的平面角为锐角,
的平面角为锐角,
∴二面![]() 角
角![]() 的余弦值为
的余弦值为![]() . —————————13分
. —————————13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, ,
, 平面
平面 与平面
与平面 角.
角. ,
, 为垂足,求证:
为垂足,求证:
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 中,底面
中,底面 是正方形,侧棱与底面垂直,
是正方形,侧棱与底面垂直, 分别是
分别是 ,
, 的中点,则以下结论中不成立的是( )
的中点,则以下结论中不成立的是( )
 与
与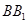 垂直
B.
垂直
B. 垂直
垂直  异面
D.
异面
D. 异面
异面  中,底面
中,底面 是正方形,侧棱与底面垂直,点
是正方形,侧棱与底面垂直,点 是正方形
是正方形 ,点
,点 ,
, 分别在
分别在 和
和 上,且
上,且 .
.
 ∥平面
∥平面 ;
; ,求
,求 的长;
的长; 的余弦值.
的余弦值.