题目内容
已知f(x)=|log3x|,若f(a)=f(b)且a≠b,则a+b的取值范围是
(2,+∞)
(2,+∞)
.分析:根据题意,先求函数f(x)的定义域,再由f(a)=f(b)可得|log3a|=|log3b|,由对数的运算性质分析可得ab=1,
又由a、b>0且a≠b,结合基本不等式的性质,可得a+b>2
=2,可得a+b的取值范围,即可得答案.
又由a、b>0且a≠b,结合基本不等式的性质,可得a+b>2
| ab |
解答:解:根据题意,对于f(x)=|log3x|,有x>0,
若f(a)=f(b),则|log3a|=|log3b|,
又由a≠b,则有log3a=-log3b,即log3a+log3b=log3ab=0,
则ab=1,
又由a、b>0且a≠b,
则a+b>2
=2,
即a+b的取值范围是(2,+∞);
故答案为(2,+∞).
若f(a)=f(b),则|log3a|=|log3b|,
又由a≠b,则有log3a=-log3b,即log3a+log3b=log3ab=0,
则ab=1,
又由a、b>0且a≠b,
则a+b>2
| ab |
即a+b的取值范围是(2,+∞);
故答案为(2,+∞).
点评:本题考查基本不等式的运用,注意a≠b的条件,即a+b=2不能成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
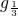 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间. [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.