题目内容
已知P是双曲线 上的点,F1、F2是其焦点,双曲线的离心率是
上的点,F1、F2是其焦点,双曲线的离心率是 的面积为9,则a+b的值为
的面积为9,则a+b的值为
- A.5
- B.6
- C.7
- D.8
C
分析:由双曲线的离心率 求得 =
= ,根据△PF1F2 的面积等于9得到|PF1|•|PF2|=18,在△PF1F2中,由勾股定理和双曲线的定义,可得b=3,从而求得a+b 的值.
,根据△PF1F2 的面积等于9得到|PF1|•|PF2|=18,在△PF1F2中,由勾股定理和双曲线的定义,可得b=3,从而求得a+b 的值.
解答:双曲线的离心率是 =
=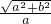 =
= ,∴
,∴ =
= .∵
.∵ ,
,
∴ ,∴△PF1F2 的面积S=
,∴△PF1F2 的面积S= |PF1|•|PF2|=9,∴|PF1|•|PF2|=18.
|PF1|•|PF2|=9,∴|PF1|•|PF2|=18.
在△PF1F2中,由勾股定理可得 4c2=|PF1|2+|PF2|2=(|PF1|-|PF2|)2+2|PF1|•|PF2|
=4a2+36,∴a2+b2=a2+9,∴b=3,∴a=4,
∴a+b=7,
故选 C.
点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用,利用双曲线的定义是解题的难点.
分析:由双曲线的离心率 求得
 =
= ,根据△PF1F2 的面积等于9得到|PF1|•|PF2|=18,在△PF1F2中,由勾股定理和双曲线的定义,可得b=3,从而求得a+b 的值.
,根据△PF1F2 的面积等于9得到|PF1|•|PF2|=18,在△PF1F2中,由勾股定理和双曲线的定义,可得b=3,从而求得a+b 的值.解答:双曲线的离心率是
 =
=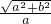 =
= ,∴
,∴ =
= .∵
.∵ ,
,∴
 ,∴△PF1F2 的面积S=
,∴△PF1F2 的面积S= |PF1|•|PF2|=9,∴|PF1|•|PF2|=18.
|PF1|•|PF2|=9,∴|PF1|•|PF2|=18.在△PF1F2中,由勾股定理可得 4c2=|PF1|2+|PF2|2=(|PF1|-|PF2|)2+2|PF1|•|PF2|
=4a2+36,∴a2+b2=a2+9,∴b=3,∴a=4,
∴a+b=7,
故选 C.
点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用,利用双曲线的定义是解题的难点.

练习册系列答案
相关题目
 上的点,F1、F2是其焦点,双曲线的离心率是
上的点,F1、F2是其焦点,双曲线的离心率是 的面积为9,则a+b的值为( )
的面积为9,则a+b的值为( ) 上的点,F1、F2是其焦点,双曲线的离心率是
上的点,F1、F2是其焦点,双曲线的离心率是 的面积为9,则a+b的值为( )
的面积为9,则a+b的值为( ) 上的点,F1、F2是其焦点,双曲线的离心率是
上的点,F1、F2是其焦点,双曲线的离心率是 的面积为9,则a+b的值为( )
的面积为9,则a+b的值为( ) 上的点,F1、F2是其焦点,双曲线的离心率是
上的点,F1、F2是其焦点,双曲线的离心率是 的面积为9,则a+b的值为
的面积为9,则a+b的值为