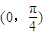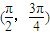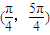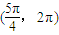题目内容
如果sin3θ-cos3θ>cosθ-sinθ,且θ∈(0,2π),那么角θ的取值范围是( )A.
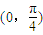
B.
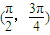
C.
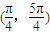
D.
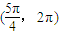
【答案】分析:先将sin3θ-cos3θ>cosθ-sinθ变形成sin3θ+sinθ>cos3θ+cosθ,然后构造函数f(x)=x3+x,将原不等式转化成f(sinθ)>f(cosθ),利用导数研究函数f(x)的单调性可得sinθ>cosθ,在θ∈(0,2π)上求出θ的取值范围即可.
解答:解:sin3θ-cos3θ>cosθ-sinθ?sin3θ+sinθ>cos3θ+cosθ.
设f(x)=x3+x∵f′(x)=3x2+1>0∴f(x)是(-∞,+∞)上的增函数,
∴原不等式?f(sinθ)>f(cosθ)?sinθ>cosθ,又∵θ∈(0,2π),
∴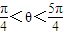 ,
,
故选C.
点评:本题为比较大小题型的拓展,函数单调性是比较大小的重要方法之一,所以这类题型都可以考虑构造函数,通过函数单调性解决问题.
解答:解:sin3θ-cos3θ>cosθ-sinθ?sin3θ+sinθ>cos3θ+cosθ.
设f(x)=x3+x∵f′(x)=3x2+1>0∴f(x)是(-∞,+∞)上的增函数,
∴原不等式?f(sinθ)>f(cosθ)?sinθ>cosθ,又∵θ∈(0,2π),
∴
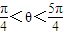 ,
,故选C.
点评:本题为比较大小题型的拓展,函数单调性是比较大小的重要方法之一,所以这类题型都可以考虑构造函数,通过函数单调性解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果sin3θ-cos3θ>cosθ-sinθ,且θ∈(0,2π),那么角θ的取值范围是( )
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|