题目内容
设a,b,c,∈R+,则“abc=1”是“![]() ”的( )
”的( )
|
| A. | 充分条件但不是必要条件 | B. | 必要条件但不是充分条件 |
|
| C. | 充分必要条件 | D. | 既不充分也不必要的条件 |
考点:
必要条件、充分条件与充要条件的判断.
专题:
计算题;压轴题.
分析:
由abc=1,推出![]() ,代入不等式的左边,证明不等式成立.利用特殊值判断不等式成立,推不出abc=1,得到结果.
,代入不等式的左边,证明不等式成立.利用特殊值判断不等式成立,推不出abc=1,得到结果.
解答:
解:因为abc=1,所以![]() ,则
,则![]() =
=![]()
=![]() ≤a+b+c.
≤a+b+c.
当a=3,b=2,c=1时,![]() 显然成立,但是abc=6≠1,
显然成立,但是abc=6≠1,
所以设a,b,c,∈R+,则“abc=1”是“![]() ”的充分条件但不是必要条件.
”的充分条件但不是必要条件.
故选A.
点评:
本题考查充要条件的应用,不等式的证明,特殊值法的应用,考查逻辑推理能力,计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
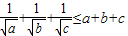 ”的( )
”的( ) ”的( )
”的( )